Code
library(tidyverse)
library(targets)
tar_source()
tar_load(c(exp3_data_agg, exp3_data))TODO: Clean-up this notebook
Define new model likelihood
One example fit:
| prop | prop_ltm | rate | gain | tau | prim_prop | deviance | convergence |
|---|---|---|---|---|---|---|---|
| 0.129707 | 0.5184667 | 0.1597853 | 42.70181 | 0.089936 | 0.9305835 | 760.8202 | 0 |
exp3_data_agg$pred <- predict(fit, exp3_data_agg, group_by = c("chunk", "gap"))
exp3_data_agg |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)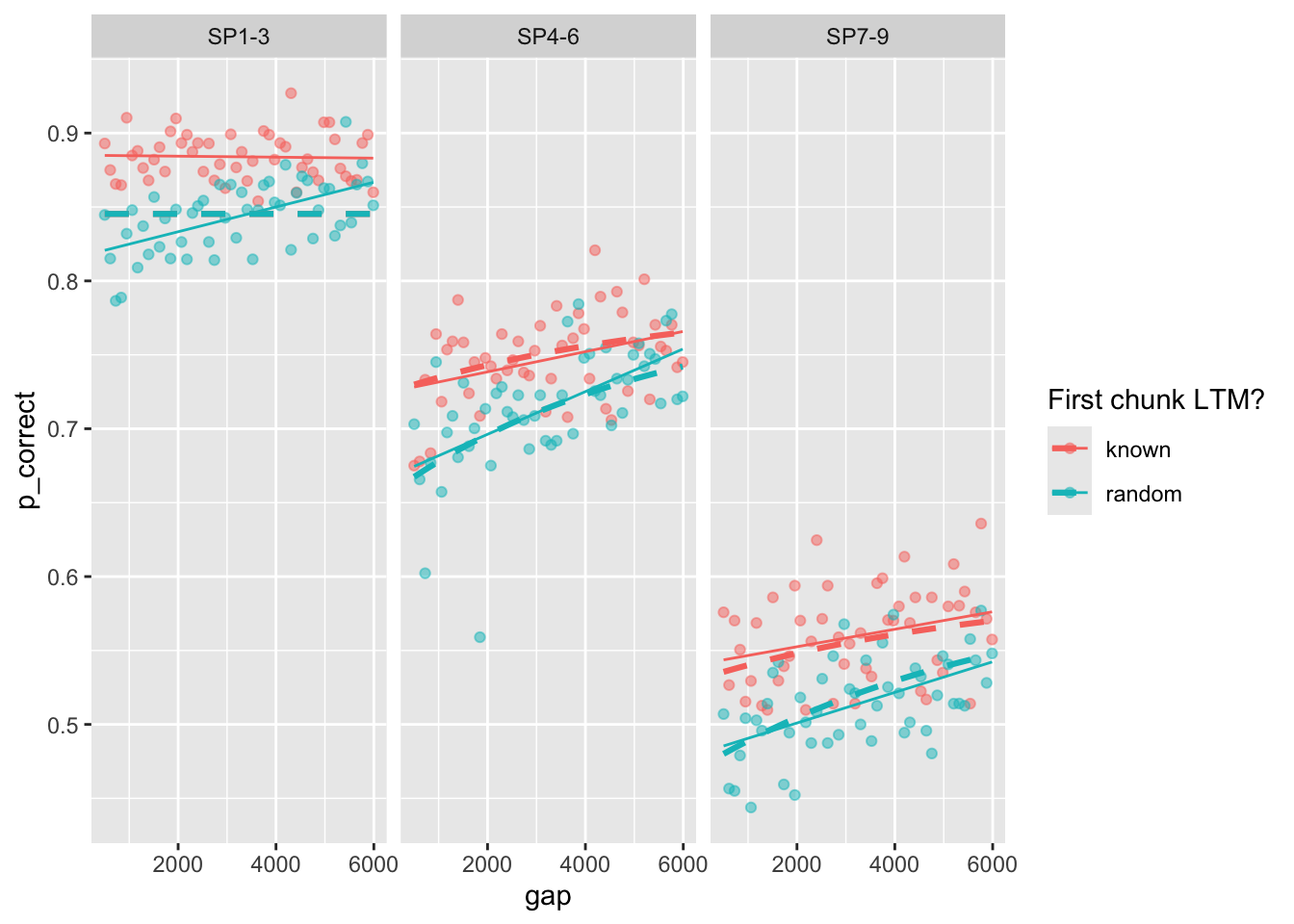
Run the estimation 100 times with different starting values:
set.seed(18)
fits <- run_or_load(
{
res <- replicate(
n = 100,
expr = estimate_model(
c(start_fun(), prim_prop = rbeta(1, 5, 2)),
exp3_data_agg,
version = 2, exclude_sp1 = T
),
simplify = FALSE
)
res <- do.call(rbind, lapply(res, optimfit_to_df))
arrange(res, deviance)
},
file = "output/exp3_fits_100_prop_primacy.rds"
)Refine the fits with a second pass starting from the best fit:
Print fits sorted by deviance:
| prop | prop_ltm | rate | gain | tau | prim_prop | deviance | convergence |
|---|---|---|---|---|---|---|---|
| 0.0830018 | 0.5354440 | 0.1521677 | 100.00000 | 0.0664134 | 0.9592183 | 1520.717 | 0 |
| 0.0830345 | 0.5354821 | 0.1522194 | 99.92881 | 0.0664355 | 0.9592133 | 1520.717 | 0 |
| 0.0827561 | 0.5303713 | 0.1540288 | 99.99304 | 0.0661689 | 0.9585271 | 1520.720 | 0 |
| 0.0833021 | 0.5326726 | 0.1534809 | 98.99042 | 0.0665430 | 0.9585757 | 1520.723 | 0 |
| 0.0836369 | 0.5354833 | 0.1524269 | 98.53729 | 0.0668022 | 0.9588923 | 1520.724 | 0 |
| 0.0838078 | 0.5349846 | 0.1527897 | 98.13969 | 0.0669035 | 0.9587414 | 1520.726 | 0 |
| 0.0839589 | 0.5352356 | 0.1523192 | 97.77404 | 0.0669837 | 0.9586211 | 1520.728 | 0 |
| 0.0840183 | 0.5344278 | 0.1528843 | 97.58774 | 0.0670162 | 0.9585227 | 1520.729 | 0 |
| 0.0840788 | 0.5337896 | 0.1528134 | 97.48065 | 0.0670620 | 0.9585533 | 1520.729 | 0 |
| 0.0843323 | 0.5352119 | 0.1524255 | 96.99083 | 0.0672207 | 0.9584937 | 1520.731 | 0 |
| 0.0844863 | 0.5384292 | 0.1511989 | 96.96959 | 0.0673687 | 0.9588990 | 1520.732 | 0 |
| 0.0841521 | 0.5333316 | 0.1531871 | 97.06339 | 0.0670524 | 0.9581341 | 1520.733 | 0 |
| 0.0850234 | 0.5387903 | 0.1513496 | 95.74477 | 0.0676811 | 0.9585429 | 1520.738 | 0 |
| 0.0854952 | 0.5374167 | 0.1511926 | 94.65133 | 0.0679400 | 0.9581097 | 1520.744 | 0 |
| 0.0853425 | 0.5370373 | 0.1515787 | 94.77365 | 0.0678094 | 0.9579259 | 1520.744 | 0 |
| 0.0854451 | 0.5350333 | 0.1525429 | 94.50061 | 0.0678727 | 0.9577814 | 1520.745 | 0 |
| 0.0857269 | 0.5368538 | 0.1515001 | 94.18233 | 0.0680980 | 0.9581038 | 1520.746 | 0 |
| 0.0872424 | 0.5390619 | 0.1510209 | 91.40748 | 0.0690687 | 0.9577849 | 1520.763 | 0 |
| 0.0878679 | 0.5354037 | 0.1524971 | 89.87321 | 0.0693818 | 0.9569372 | 1520.771 | 0 |
| 0.0880266 | 0.5353644 | 0.1539354 | 89.55011 | 0.0694815 | 0.9567853 | 1520.778 | 0 |
| 0.0884297 | 0.5360268 | 0.1513224 | 88.72862 | 0.0696856 | 0.9565830 | 1520.779 | 0 |
| 0.0878443 | 0.5251040 | 0.1565616 | 89.02264 | 0.0691813 | 0.9553297 | 1520.786 | 0 |
| 0.0892337 | 0.5399017 | 0.1496270 | 87.49761 | 0.0702117 | 0.9566977 | 1520.788 | 0 |
| 0.0896874 | 0.5467911 | 0.1466649 | 86.80853 | 0.0704719 | 0.9567592 | 1520.802 | 0 |
| 0.0915173 | 0.5403781 | 0.1506760 | 83.44070 | 0.0715516 | 0.9554777 | 1520.814 | 0 |
| 0.0915863 | 0.5467830 | 0.1481750 | 83.97125 | 0.0717513 | 0.9567280 | 1520.815 | 0 |
| 0.0907884 | 0.5516159 | 0.1462604 | 85.63544 | 0.0713531 | 0.9578251 | 1520.816 | 0 |
| 0.0904884 | 0.5308324 | 0.1531446 | 84.52523 | 0.0708115 | 0.9548965 | 1520.819 | 0 |
| 0.0921162 | 0.5379638 | 0.1511176 | 82.15251 | 0.0718255 | 0.9546897 | 1520.824 | 0 |
| 0.0934299 | 0.5461201 | 0.1483120 | 80.77434 | 0.0727898 | 0.9556430 | 1520.837 | 0 |
| 0.0936599 | 0.5373178 | 0.1509119 | 79.91900 | 0.0728257 | 0.9546394 | 1520.847 | 0 |
| 0.0934048 | 0.5373752 | 0.1522977 | 79.64859 | 0.0724489 | 0.9532476 | 1520.856 | 0 |
| 0.0954108 | 0.5338564 | 0.1530252 | 76.62310 | 0.0736285 | 0.9523789 | 1520.874 | 0 |
| 0.0964956 | 0.5497604 | 0.1470154 | 76.30653 | 0.0746150 | 0.9547932 | 1520.879 | 0 |
| 0.0917041 | 0.5584003 | 0.1470930 | 83.85527 | 0.0717872 | 0.9566873 | 1520.882 | 0 |
| 0.0973273 | 0.5302367 | 0.1539601 | 73.54802 | 0.0746042 | 0.9507225 | 1520.911 | 0 |
| 0.0987585 | 0.5460551 | 0.1491697 | 72.64034 | 0.0757628 | 0.9528200 | 1520.913 | 0 |
| 0.0987959 | 0.5381743 | 0.1510308 | 71.89543 | 0.0755197 | 0.9509666 | 1520.921 | 0 |
| 0.1007429 | 0.5473097 | 0.1478690 | 70.29082 | 0.0769701 | 0.9526443 | 1520.941 | 0 |
| 0.1031380 | 0.5365476 | 0.1515734 | 66.21486 | 0.0778125 | 0.9484016 | 1520.993 | 0 |
| 0.1041868 | 0.5425277 | 0.1497028 | 65.23047 | 0.0784592 | 0.9486410 | 1521.005 | 0 |
| 0.1041107 | 0.5585138 | 0.1426450 | 66.85880 | 0.0790617 | 0.9531637 | 1521.005 | 0 |
| 0.1052323 | 0.5522870 | 0.1466097 | 65.03940 | 0.0794905 | 0.9512479 | 1521.012 | 0 |
| 0.1032888 | 0.5270420 | 0.1553102 | 65.66822 | 0.0777932 | 0.9473241 | 1521.014 | 0 |
| 0.1050829 | 0.5429193 | 0.1493026 | 64.45731 | 0.0790327 | 0.9487062 | 1521.016 | 0 |
| 0.1055747 | 0.5453514 | 0.1495319 | 64.38901 | 0.0795725 | 0.9500933 | 1521.017 | 0 |
| 0.1057176 | 0.5363009 | 0.1519290 | 63.21499 | 0.0791567 | 0.9469873 | 1521.037 | 0 |
| 0.1056761 | 0.5328284 | 0.1528260 | 63.19574 | 0.0791423 | 0.9469534 | 1521.040 | 0 |
| 0.1095031 | 0.5597043 | 0.1427385 | 60.18882 | 0.0814623 | 0.9482292 | 1521.102 | 0 |
| 0.1038245 | 0.5178414 | 0.1606086 | 64.11113 | 0.0776493 | 0.9440227 | 1521.108 | 0 |
| 0.1112165 | 0.5405131 | 0.1513658 | 57.83141 | 0.0821252 | 0.9451479 | 1521.121 | 0 |
| 0.1139487 | 0.5665163 | 0.1408282 | 56.79748 | 0.0842963 | 0.9495305 | 1521.163 | 0 |
| 0.1150464 | 0.5620415 | 0.1424970 | 55.49423 | 0.0846745 | 0.9478959 | 1521.174 | 0 |
| 0.1104956 | 0.5844357 | 0.1330230 | 61.23827 | 0.0830523 | 0.9550584 | 1521.176 | 0 |
| 0.1150277 | 0.5707915 | 0.1394673 | 56.13136 | 0.0850230 | 0.9502024 | 1521.195 | 0 |
| 0.1168787 | 0.5563987 | 0.1475113 | 53.57138 | 0.0854354 | 0.9456710 | 1521.224 | 0 |
| 0.1170302 | 0.5467398 | 0.1477255 | 52.79237 | 0.0850381 | 0.9430341 | 1521.225 | 0 |
| 0.1190151 | 0.5745878 | 0.1375233 | 52.76130 | 0.0870007 | 0.9487474 | 1521.265 | 0 |
| 0.1180843 | 0.5374202 | 0.1543369 | 51.51058 | 0.0853142 | 0.9404624 | 1521.282 | 0 |
| 0.1206378 | 0.5369294 | 0.1526183 | 49.75313 | 0.0867212 | 0.9404126 | 1521.311 | 0 |
| 0.1222813 | 0.5450775 | 0.1484505 | 48.58462 | 0.0874118 | 0.9398335 | 1521.338 | 0 |
| 0.1219608 | 0.5950076 | 0.1293583 | 51.47250 | 0.0890850 | 0.9520846 | 1521.387 | 0 |
| 0.1258652 | 0.5543236 | 0.1449665 | 46.47660 | 0.0893696 | 0.9402240 | 1521.393 | 0 |
| 0.1261358 | 0.5512622 | 0.1469249 | 46.15517 | 0.0893986 | 0.9393450 | 1521.405 | 0 |
| 0.1229203 | 0.6004439 | 0.1274795 | 51.09406 | 0.0898015 | 0.9532568 | 1521.437 | 0 |
| 0.1253455 | 0.5347543 | 0.1524909 | 45.93500 | 0.0884188 | 0.9358299 | 1521.453 | 0 |
| 0.1096435 | 0.6245279 | 0.1157842 | 65.14104 | 0.0838056 | 0.9644263 | 1521.465 | 0 |
| 0.1291902 | 0.5698808 | 0.1404231 | 44.52248 | 0.0909739 | 0.9401136 | 1521.507 | 0 |
| 0.1316542 | 0.5861278 | 0.1329112 | 44.07969 | 0.0930474 | 0.9448045 | 1521.528 | 0 |
| 0.1320240 | 0.5487744 | 0.1460666 | 42.47430 | 0.0920422 | 0.9368930 | 1521.552 | 0 |
| 0.1407647 | 0.5726243 | 0.1378135 | 38.67907 | 0.0966723 | 0.9386590 | 1521.727 | 0 |
| 0.1410802 | 0.5921934 | 0.1299198 | 39.08275 | 0.0972915 | 0.9421512 | 1521.746 | 0 |
| 0.1416289 | 0.5584553 | 0.1449145 | 37.55499 | 0.0961602 | 0.9331385 | 1521.772 | 0 |
| 0.1442493 | 0.5817889 | 0.1357689 | 37.16069 | 0.0981666 | 0.9379234 | 1521.805 | 0 |
| 0.1485820 | 0.5506684 | 0.1476578 | 34.44050 | 0.0989464 | 0.9297136 | 1521.974 | 0 |
| 0.1335032 | 0.4896621 | 0.1771724 | 40.02027 | 0.0912584 | 0.9248692 | 1522.027 | 0 |
| 0.1508329 | 0.5659537 | 0.1397505 | 33.56548 | 0.0994088 | 0.9283791 | 1522.043 | 0 |
| 0.1464991 | 0.6365233 | 0.1119736 | 38.25589 | 0.1015555 | 0.9525763 | 1522.066 | 0 |
| 0.1570901 | 0.5720074 | 0.1369226 | 31.39721 | 0.1020279 | 0.9277262 | 1522.192 | 0 |
| 0.1578781 | 0.5796311 | 0.1354878 | 31.28607 | 0.1025839 | 0.9289186 | 1522.195 | 0 |
| 0.1557528 | 0.5623220 | 0.1426612 | 31.36372 | 0.1005411 | 0.9230903 | 1522.254 | 0 |
| 0.1615952 | 0.5661500 | 0.1440328 | 29.91051 | 0.1040553 | 0.9264082 | 1522.330 | 0 |
| 0.1625162 | 0.5859924 | 0.1360934 | 29.80458 | 0.1043471 | 0.9275039 | 1522.355 | 0 |
| 0.1643793 | 0.6202930 | 0.1195451 | 30.34787 | 0.1072577 | 0.9396434 | 1522.388 | 0 |
| 0.1628606 | 0.6659198 | 0.1026569 | 32.71971 | 0.1100000 | 0.9576486 | 1522.606 | 0 |
| 0.1673065 | 0.5570623 | 0.1476521 | 27.42337 | 0.1035436 | 0.9131497 | 1522.795 | 0 |
| 0.1494665 | 0.7064391 | 0.0870326 | 40.84013 | 0.1073822 | 0.9772426 | 1522.822 | 0 |
| 0.1757971 | 0.5737036 | 0.1355153 | 25.60590 | 0.1074592 | 0.9172798 | 1522.859 | 0 |
| 0.1237810 | 0.7275594 | 0.0803559 | 60.88937 | 0.0958362 | 0.9892582 | 1522.916 | 0 |
| 0.1478485 | 0.7136234 | 0.0842819 | 42.33303 | 0.1072880 | 0.9809562 | 1522.918 | 0 |
| 0.1508772 | 0.7128888 | 0.0843160 | 40.69104 | 0.1086132 | 0.9801147 | 1522.946 | 0 |
| 0.1641892 | 0.5166694 | 0.1581206 | 27.52562 | 0.1009010 | 0.9058324 | 1522.977 | 0 |
| 0.1454702 | 0.7272316 | 0.0801023 | 44.59122 | 0.1069657 | 0.9859114 | 1523.054 | 0 |
| 0.1560018 | 0.7256169 | 0.0812223 | 39.04160 | 0.1118570 | 0.9840110 | 1523.160 | 0 |
| 0.1008613 | 0.7540632 | 0.0701410 | 95.94044 | 0.0832805 | 0.9999999 | 1523.350 | 0 |
| 0.1500814 | 0.7543605 | 0.0712736 | 44.53389 | 0.1115246 | 0.9976890 | 1523.548 | 0 |
| 0.2012512 | 0.6942274 | 0.0925222 | 22.99875 | 0.1245127 | 0.9570987 | 1523.700 | 0 |
| 0.1954065 | 0.5381045 | 0.1690204 | 21.11082 | 0.1135602 | 0.9050614 | 1524.333 | 0 |
| 0.2222245 | 0.7091319 | 0.0886436 | 19.79598 | 0.1324736 | 0.9621327 | 1524.418 | 0 |
| 0.2420613 | 0.7426193 | 0.0755768 | 17.80195 | 0.1411300 | 0.9779758 | 1525.069 | 0 |
Not as much variance as I thought there would be. Let’s limit to the fits within 2 deviance units of the best fit:
Here is the distribution of parameter values that are within 2 deviance units of the best fit:
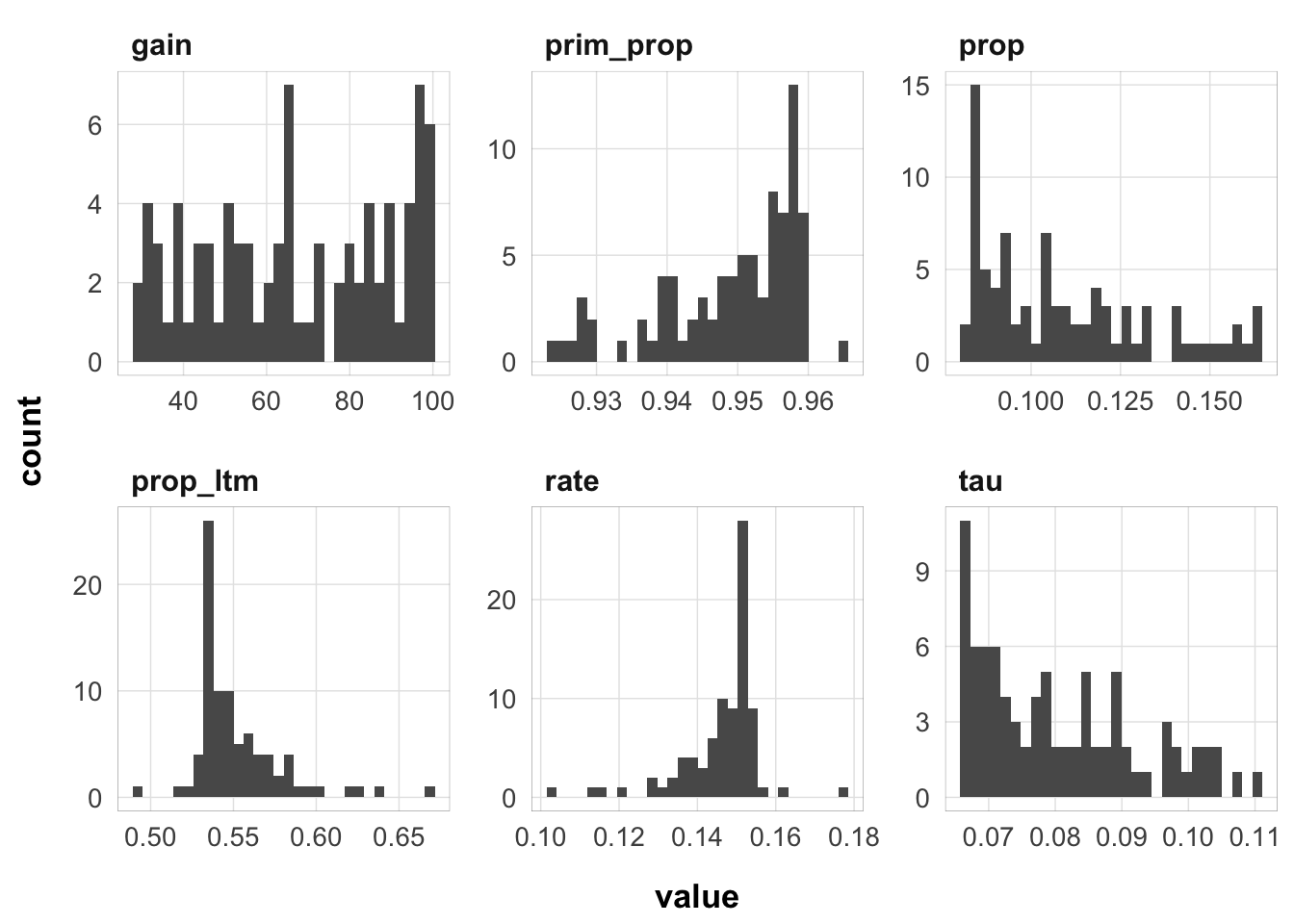
Here is the plot of the best fitting model:
best_fit <- estimate_model(unlist(best_fits[1, 1:6]), exp3_data_agg, version = 2, exclude_sp1 = T)
exp3_data_agg$pred <- predict(best_fit, exp3_data_agg, group_by = c("chunk", "gap"))
exp3_data_agg |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)`geom_smooth()` using formula = 'y ~ x'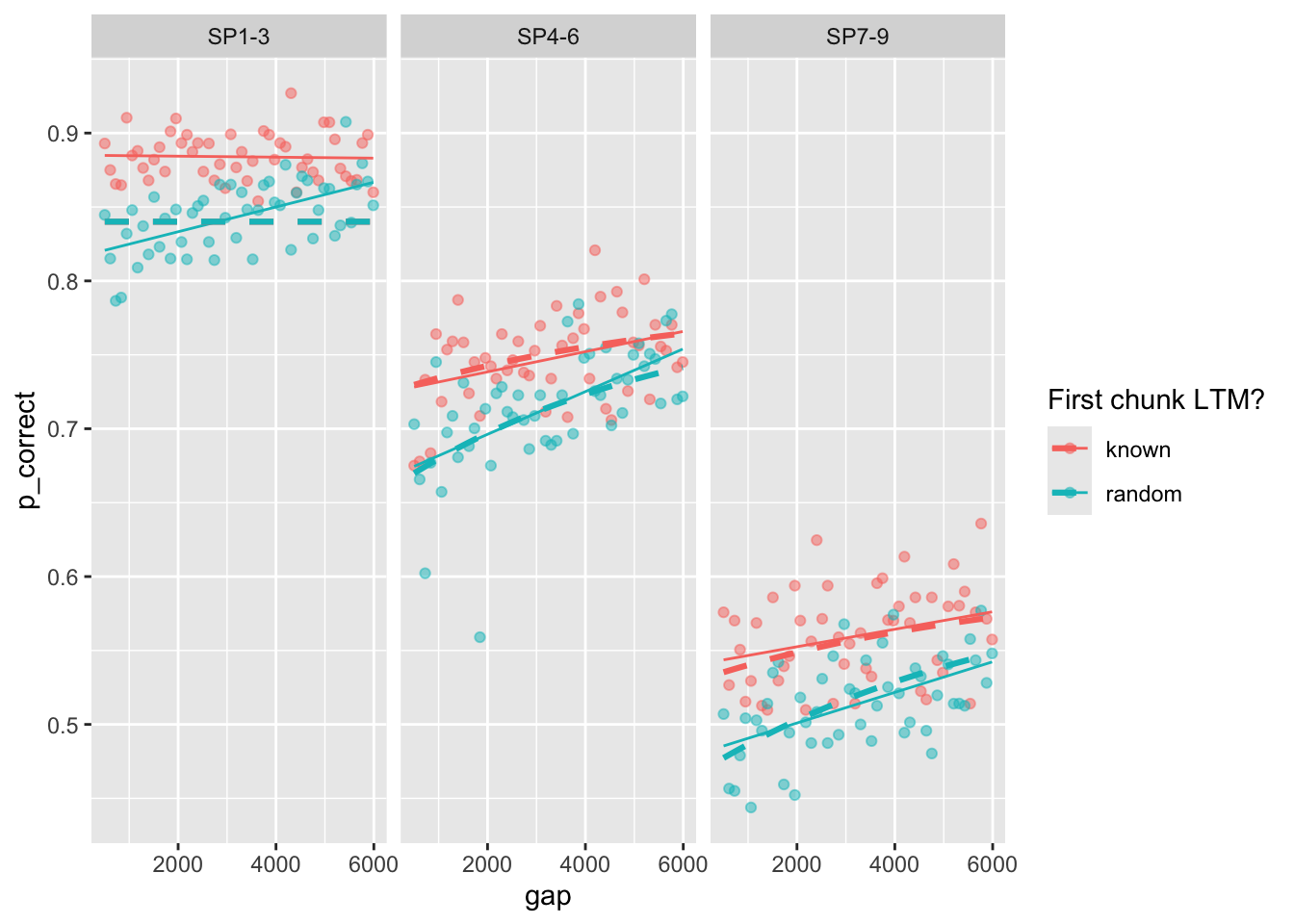
and the parameter estimates:
| prop | prop_ltm | rate | gain | tau | prim_prop | |
|---|---|---|---|---|---|---|
| x | 0.0827601 | 0.5305627 | 0.1540501 | 99.99801 | 0.0661733 | 0.958538 |
with this rate, the resource recovery over time looks like this:
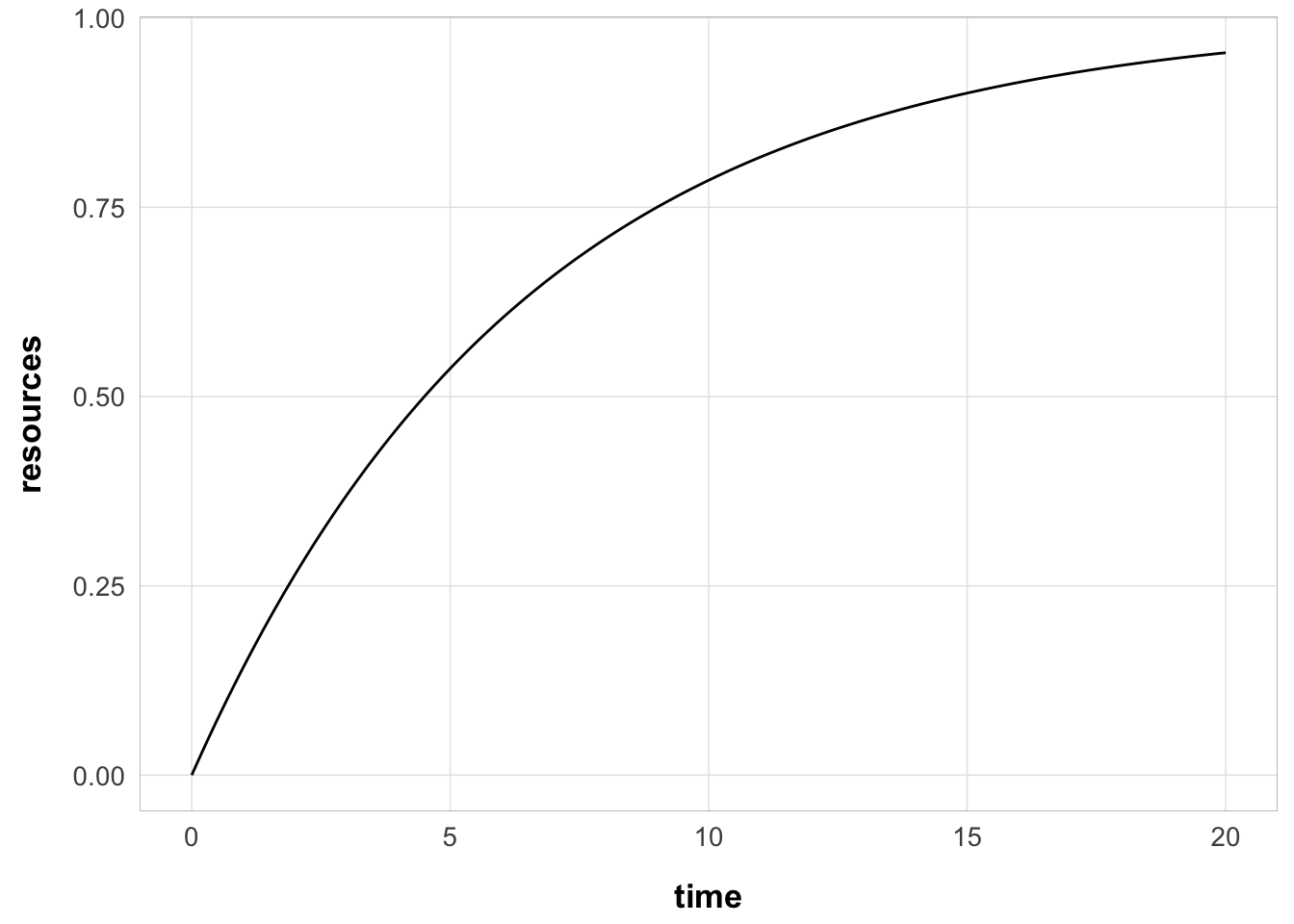
with 50% of the resource recovered after 4.5 seconds
and 25% of the resource recovered after 1.87 seconds
Calculate the total recall period duration on each trial:
`summarise()` has grouped output by 'id'. You can override using the `.groups` argument.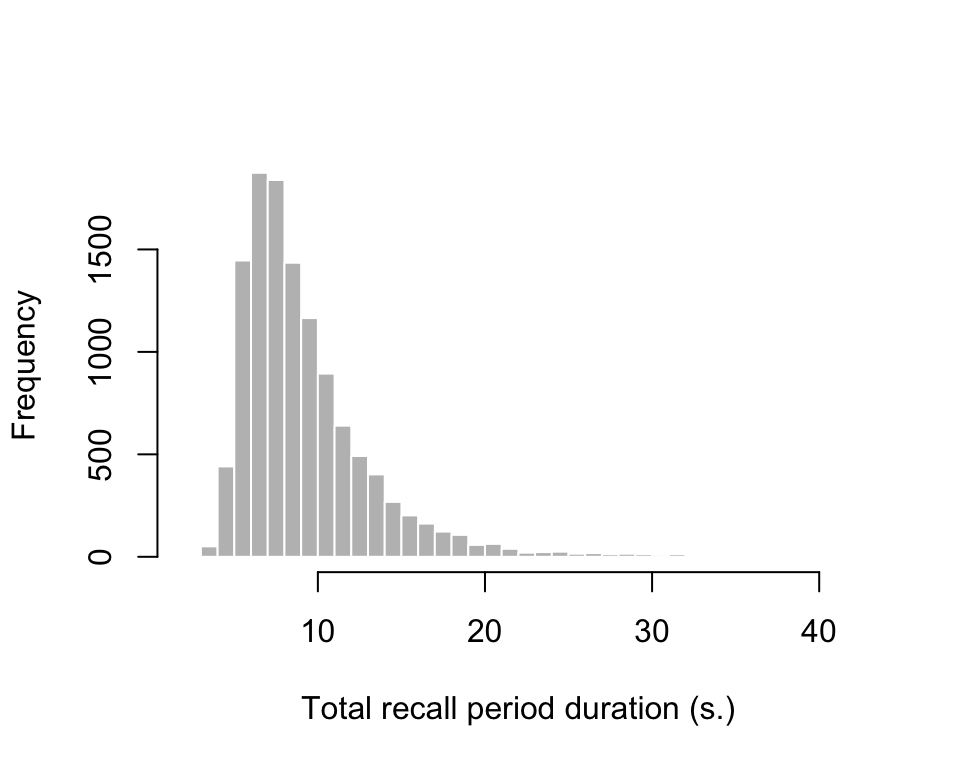
Create the trial structure for the simulation:
exp3_trial_str <- run_or_load({
exp3_data |>
group_by(id, trial) |>
do({
aggregate_data(.)
})
}, file = "output/exp3_trial_structure.rds")
exp3_trial_str <- left_join(exp3_trial_str, total_rts) |>
mutate(ISI = ifelse(itemtype == "SP7-9", total_recall_duration, ISI),
ser_pos = case_when(
itemtype == "SP1-3" ~ 1,
itemtype == "SP4-6" ~ 2,
itemtype == "SP7-9" ~ 3
))Run the model without resetting the resource at the start of each trial:
serial_recall_full <- function(
setsize, ISI = rep(0.5, setsize), item_in_ltm = rep(TRUE, setsize), ser_pos = 1:setsize,
prop = 0.2, prop_ltm = 0.5, tau = 0.15, gain = 25, rate = 0.1, prim_prop = 1,
r_max = 1, lambda = 1, growth = "linear") {
R <- r_max
p_recall <- vector("numeric", length = setsize)
prop_ltm <- ifelse(item_in_ltm, prop_ltm, 1)
for (item in 1:setsize) {
# strength of the item and recall probability
strength <- (prop * R)^lambda * prim_prop^(ser_pos[item] - 1)
p_recall[item] <- 1 / (1 + exp(-(strength - tau) * gain))
# amount of resources consumed by the item
r_cost <- strength^(1 / lambda) * prop_ltm[item]
R <- R - r_cost
# recover resources
R <- switch(growth,
"linear" = min(r_max, R + rate * ISI[item]),
"asy" = R + (r_max - R) * (1 - exp(-rate * ISI[item]))
)
}
p_recall
}
subj1 <- exp3_trial_str |>
filter(id == 44125)Here it is for one example subject:
subj1$pred <- serial_recall_full(
setsize = nrow(subj1),
ISI = subj1$ISI,
item_in_ltm = subj1$item_in_ltm,
ser_pos = subj1$ser_pos,
prop = best_fit$par["prop"],
prop_ltm = best_fit$par["prop_ltm"],
tau = best_fit$par["tau"],
gain = best_fit$par["gain"],
rate = best_fit$par["rate"],
prim_prop = best_fit$par["prim_prop"],
growth = "asy"
)
subj1 |>
ungroup() |>
mutate(absolute_position = 1:n()) |>
ggplot(aes(x = absolute_position, y = pred)) +
geom_point() +
geom_line() +
theme_pub()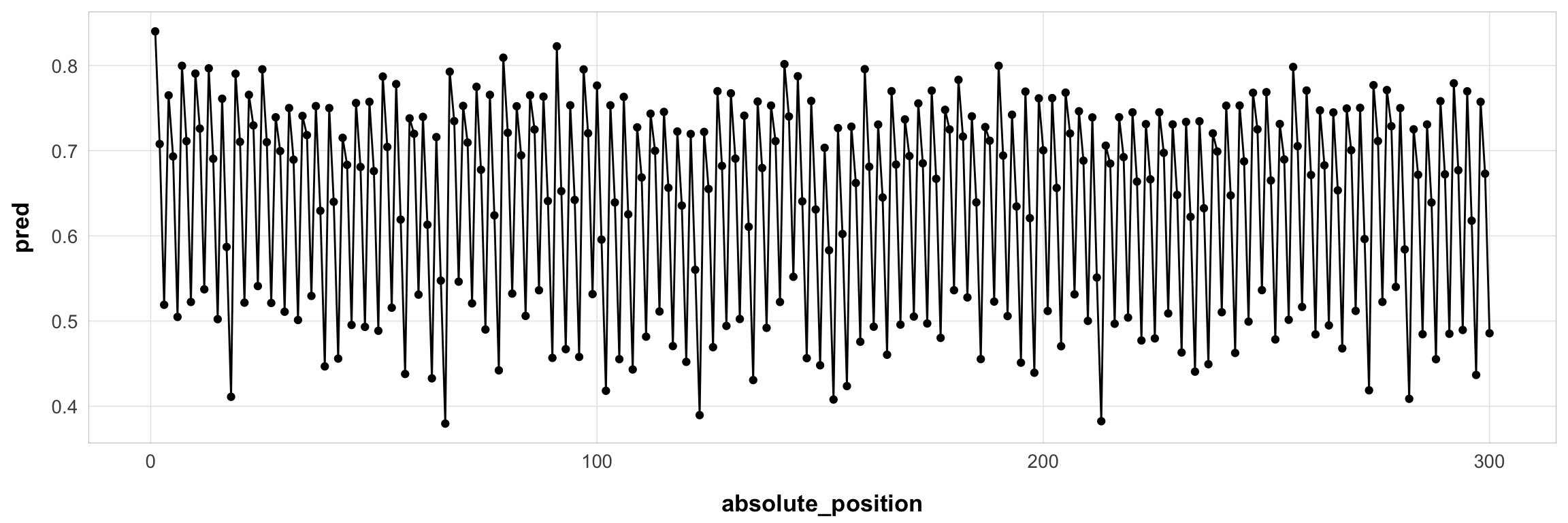
Same, but collapsed over serial position (one value per trial):
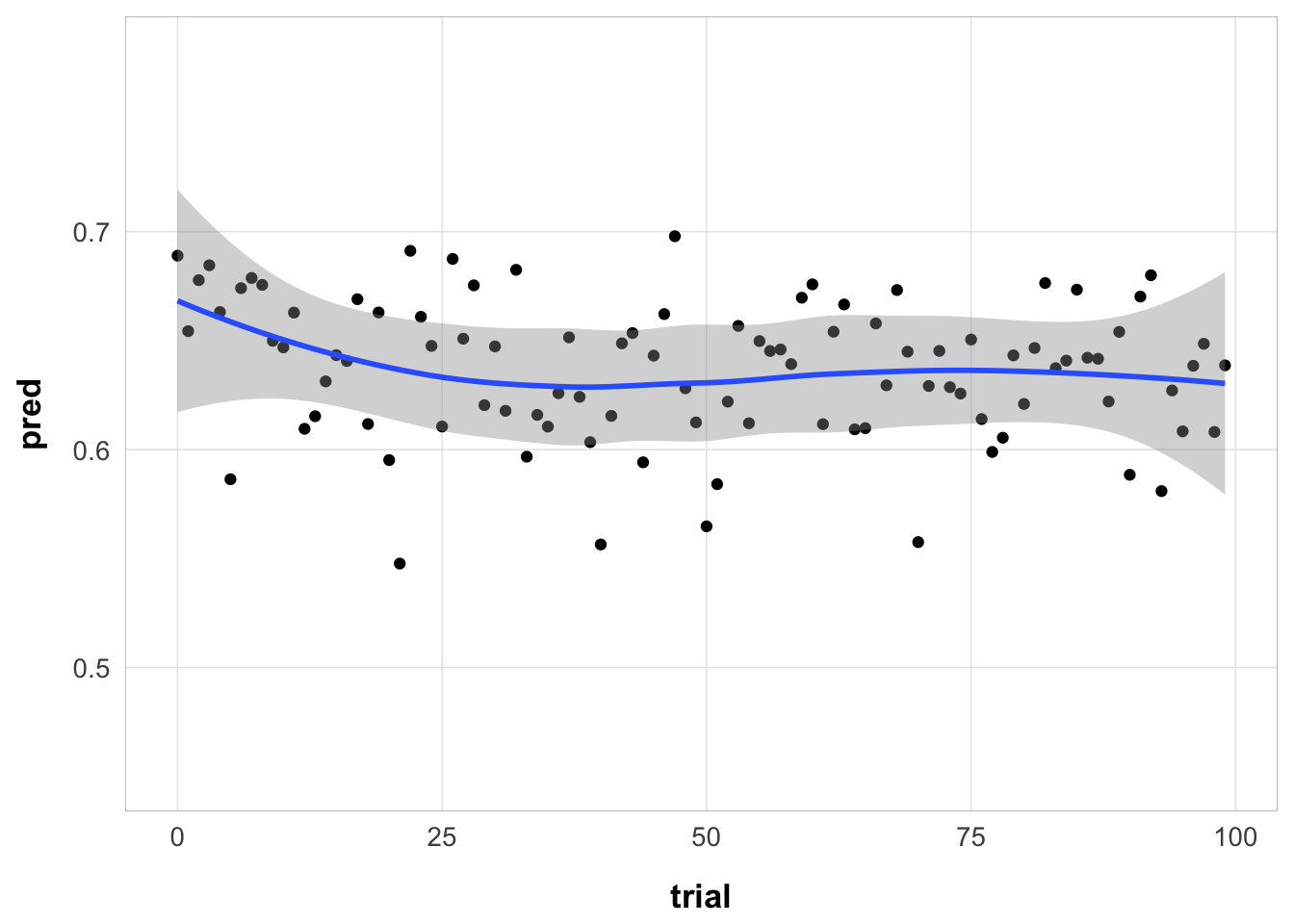
Now simulate the full dataset:
sim_no_reset_full <- function(data, best_fit) {
data |>
group_by(id) |>
mutate(pred = serial_recall_full(
setsize = n(),
ISI = ISI,
item_in_ltm = item_in_ltm,
ser_pos = ser_pos,
prop = best_fit$par["prop"],
prop_ltm = best_fit$par["prop_ltm"],
tau = best_fit$par["tau"],
gain = best_fit$par["gain"],
rate = best_fit$par["rate"],
prim_prop = best_fit$par["prim_prop"],
growth = "asy"
))
}
full_sim <- sim_no_reset_full(exp3_trial_str, best_fit)
ggplot(full_sim, aes(x = trial, y = pred)) +
stat_summary() +
geom_smooth() +
theme_pub()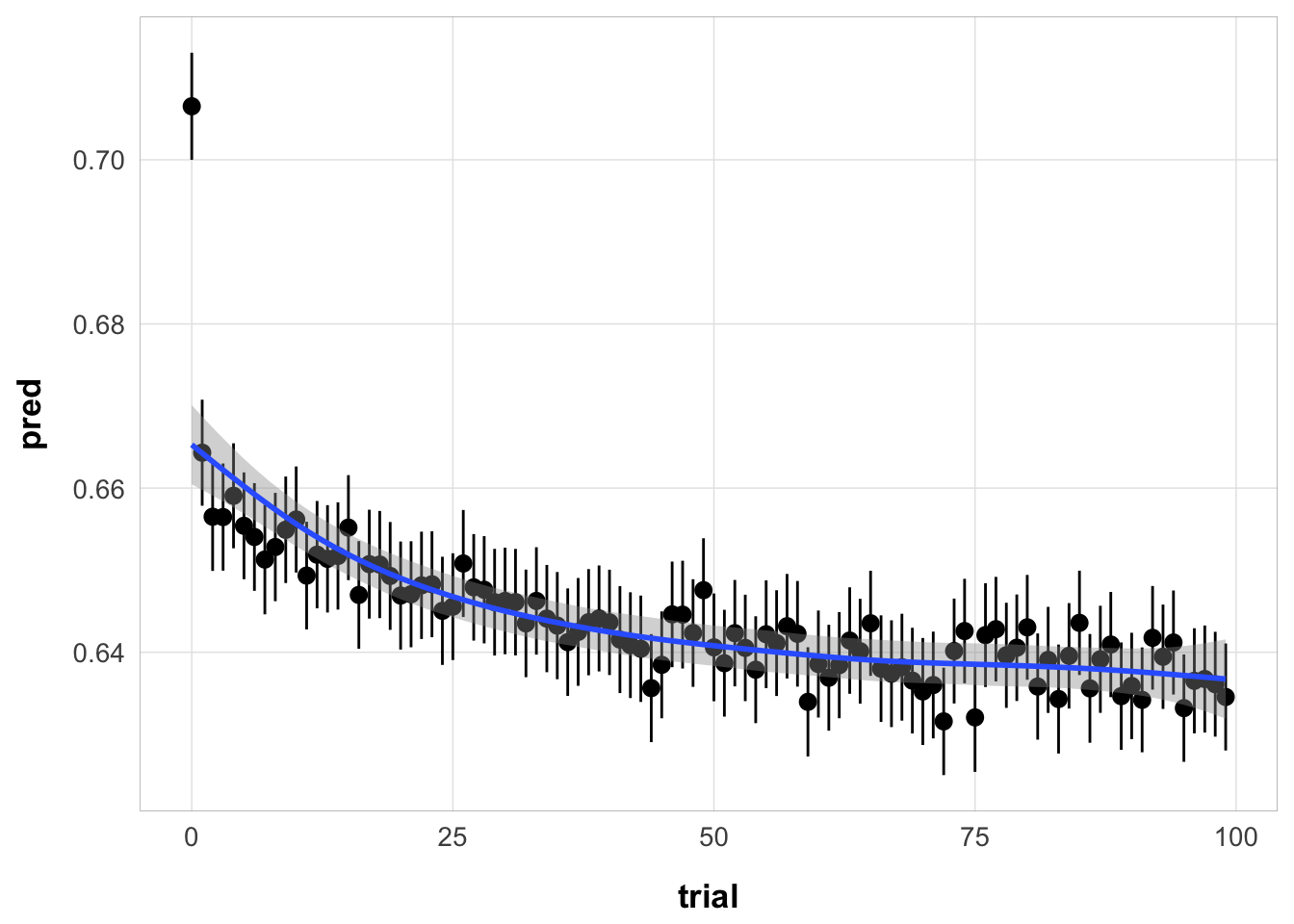
Yes, the model predicts worsening performance over trials, but the effect is miniscule.
Plot the original predictions recomputed with the full trial-by-trial model:
full_sim |>
group_by(chunk, gap, itemtype) |>
summarize(pred = mean(pred),
p_correct = mean(p_correct)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)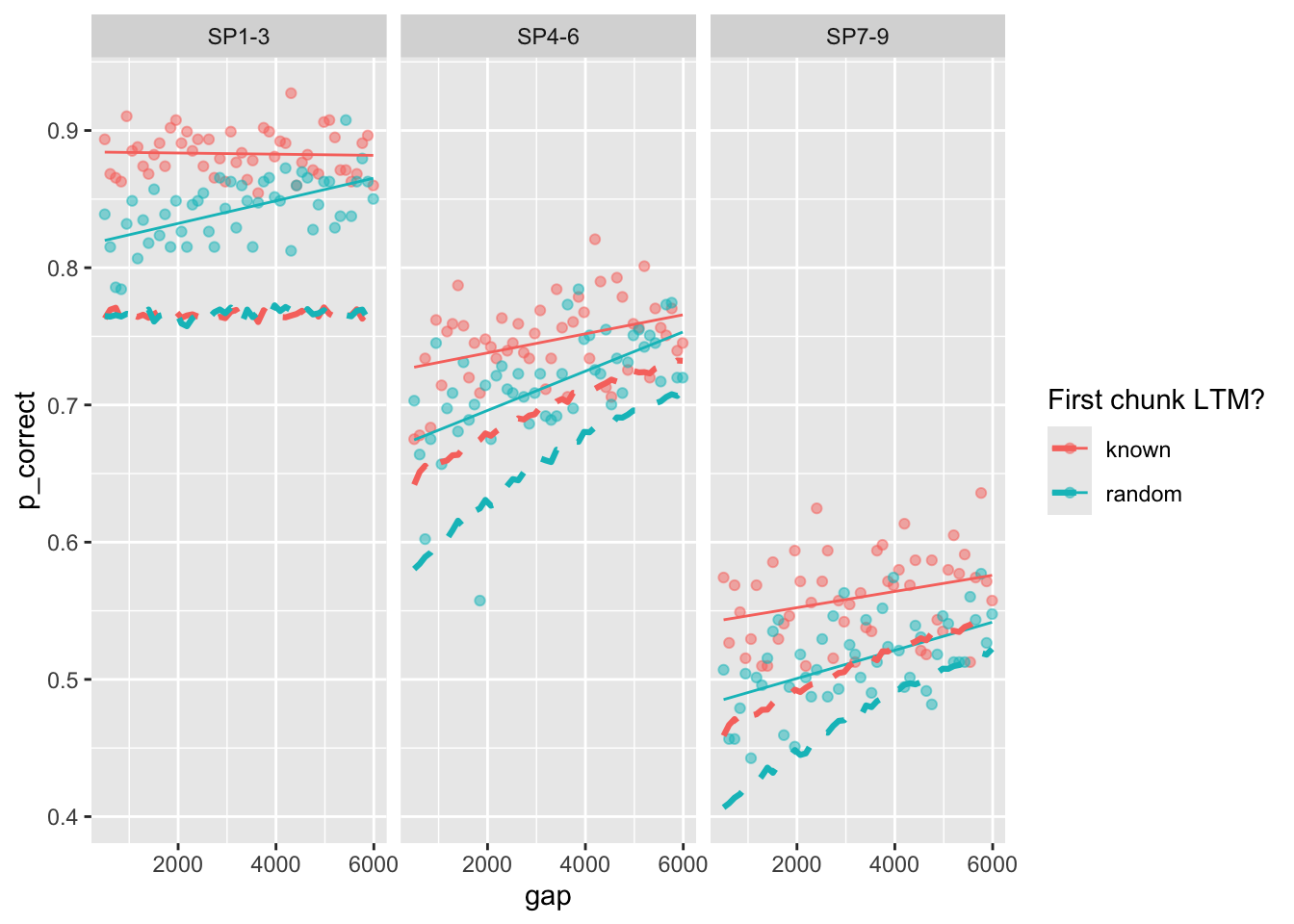
exp3_trial_str <- run_or_load(
{
exp3_data |>
group_by(id, trial) |>
do({
aggregate_data(.)
})
},
file = "output/exp3_trial_structure.rds"
)
exp3_trial_str <- exp3_trial_str |>
mutate(
ISI = ifelse(itemtype == "SP7-9", 9 * 0.2 + 1, ISI),
ser_pos = case_when(
itemtype == "SP1-3" ~ 1,
itemtype == "SP4-6" ~ 2,
itemtype == "SP7-9" ~ 3
)
)
full_sim_v2 <- sim_no_reset_full(exp3_trial_str, best_fit)
ggplot(full_sim_v2, aes(x = trial, y = pred)) +
stat_summary() +
theme_pub()No summary function supplied, defaulting to `mean_se()`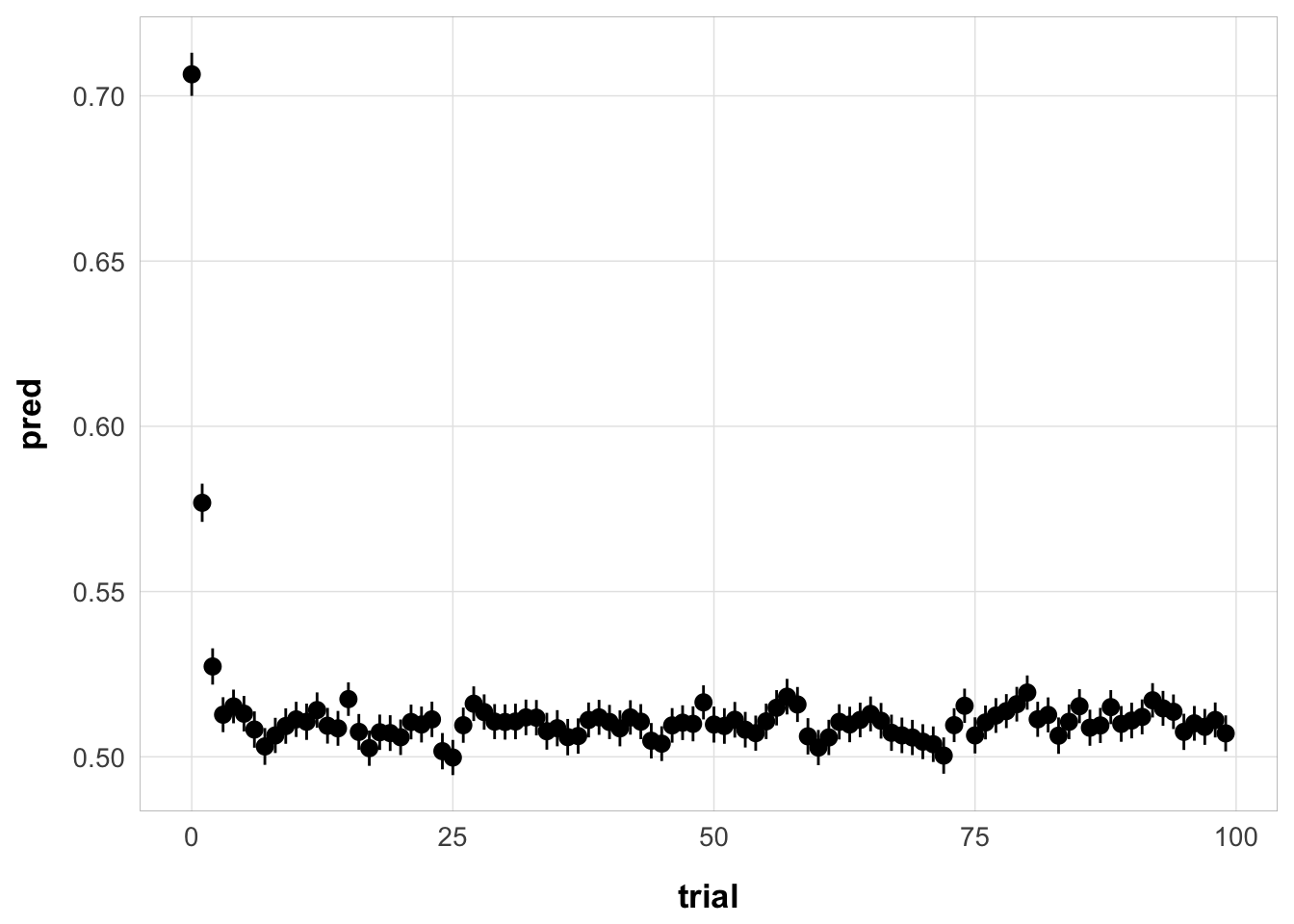
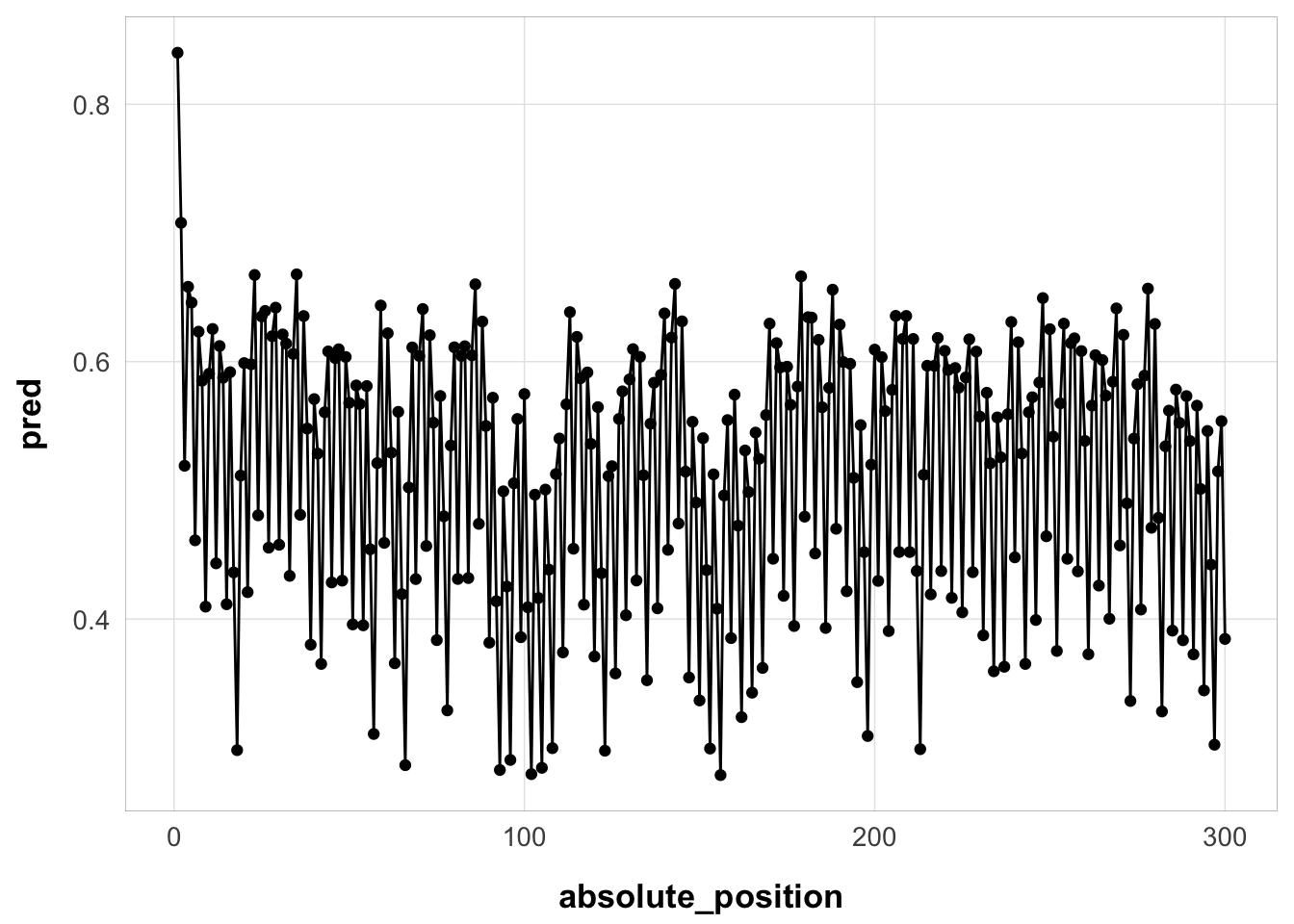
full_sim_v2 |>
group_by(chunk, gap, itemtype) |>
summarize(pred = mean(pred),
p_correct = mean(p_correct)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)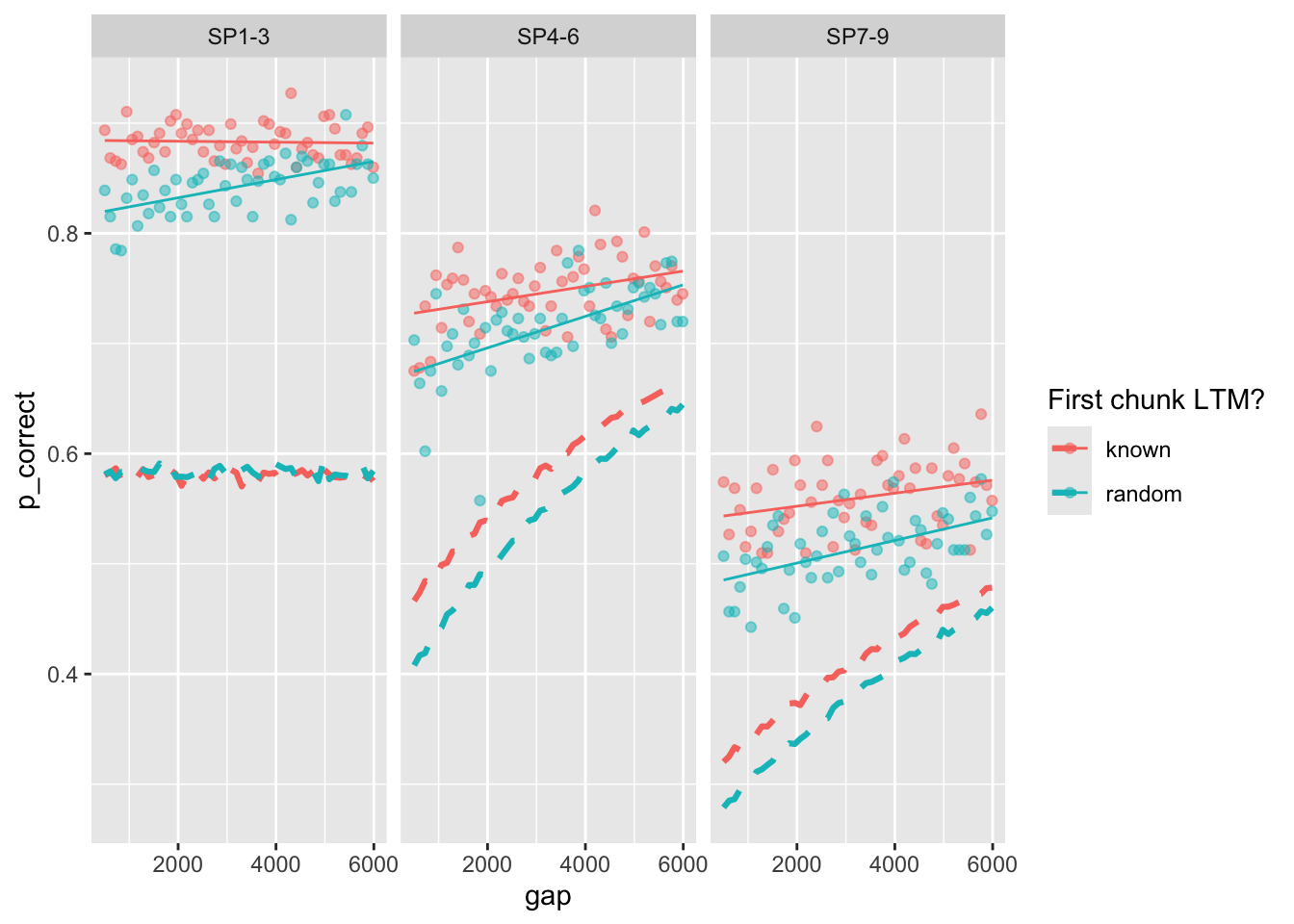
---
title: "Extra primacy parameter"
format: html
---
TODO: Clean-up this notebook
```{r}
#| label: init
#| message: false
library(tidyverse)
library(targets)
tar_source()
tar_load(c(exp3_data_agg, exp3_data))
```
Define new model likelihood
```{r, include = FALSE}
serial_recall_v2 <- function(
setsize, ISI = rep(0.5, setsize), item_in_ltm = rep(TRUE, setsize),
prop = 0.2, prop_ltm = 0.5, tau = 0.15, gain = 25, rate = 0.1, prim_prop = 1,
r_max = 1, lambda = 1, growth = "linear") {
w1 <- 1 - (1 - prop_ltm) * item_in_ltm[1]
psq <- prop^2
tmp <- w1 * exp(-rate * ISI[1]) * psq
tmp2 <- exp(-rate * ISI[2])
s <- c(
prop,
(prop - tmp) * prim_prop,
(prop - tmp * (1 - prop) * tmp2 - psq * tmp2) * prim_prop^2
)
p_recall <- 1 / (1 + exp(-gain * (s - tau)))
p_recall
}
calcdev <- function(params, dat, exclude_sp1 = FALSE, version = 2, ...) {
if (version == 1) {
pred <- serial_recall(
setsize = 3,
ISI = dat$ISI,
item_in_ltm = dat$item_in_ltm,
prop = params["prop"],
prop_ltm = params["prop_ltm"],
tau = params["tau"],
gain = params["gain"],
rate = params["rate"],
...
)
} else {
pred <- serial_recall_v2(
setsize = 3,
ISI = dat$ISI,
item_in_ltm = dat$item_in_ltm,
prop = params["prop"],
prop_ltm = params["prop_ltm"],
tau = params["tau"],
gain = params["gain"],
rate = params["rate"],
prim_prop = params["prim_prop"],
...
)
}
log_lik <- dbinom(dat$n_correct, dat$n_total, prob = pred, log = TRUE)
if (exclude_sp1) {
log_lik <- log_lik[-1]
}
-sum(log_lik)
}
overall_deviance <- function(params, split_data, ...,
priors = list()) {
dev <- unlist(lapply(split_data, function(x) calcdev(params, x, ...)))
out <- sum(dev)
if (length(priors) > 0) {
pnames <- names(priors)
for (i in seq_along(priors)) {
out <- out - dnorm(params[pnames[i]], mean = priors[[i]]$mean, sd = priors[[i]]$sd, log = TRUE)
}
}
out
}
estimate_model <- function(start, data, two_step = FALSE, priors = list(), simplify = FALSE, by = c("chunk", "gap"), ...) {
# internal helper functions
constrain_pars <- function(par) {
par[c("prop", "prop_ltm", "tau", "rate", "prim_prop")] <- inv_logit(par[c("prop", "prop_ltm", "tau", "rate", "prim_prop")])
par["gain"] <- inv_logit(par["gain"], lb = 0, ub = 100)
par
}
unconstrain_pars <- function(par) {
par[c("prop", "prop_ltm", "tau", "rate", "prim_prop")] <- logit(par[c("prop", "prop_ltm", "tau", "rate", "prim_prop")])
par["gain"] <- logit(par["gain"], lb = 0, ub = 100)
par
}
fn <- function(par, split_data, par2 = NULL, ...) {
par <- c(par, par2)
par <- constrain_pars(par)
overall_deviance(par, split_data, ...)
}
start_uc <- unconstrain_pars(start)
# if two_step is TRUE, nest the optimization (prop, prop_ltm, and rate) within the outer optimization (tau, gain)
if (two_step) {
start1 <- start_uc[c("prop", "prop_ltm", "rate", "prim_prop")]
start2 <- start_uc[c("tau", "gain")]
fn2 <- function(par, split_data, par2, ...) {
fit <- optim(
par = par2,
fn = fn,
split_data = split_data,
control = list(maxit = 1e6),
par2 = par,
...
)
environment(fn)$fit_inner <- fit
fit$value
}
} else {
start1 <- start_uc
start2 <- NULL
fn2 <- fn
}
groups <- interaction(data[, by])
split_data <- split(data, groups)
fit <- optim(
par = start1,
fn = fn2,
split_data = split_data,
control = list(maxit = 1e6),
par2 = start2,
priors = priors,
...
)
est <- fit$par
convergence <- fit$convergence
value <- fit$value
counts <- fit$counts
if (two_step) {
est <- c(est, fit_inner$par)
concergence <- convergence + fit_inner$convergence
counts <- counts + fit_inner$counts
}
# return the estimated parameters
est <- constrain_pars(est)
class(est) <- "serial_recall_pars"
fit <- structure(
list(
start = start,
par = est,
convergence = convergence,
counts = counts,
value = value
),
class = "serial_recall_fit"
)
if (simplify) {
out <- optimfit_to_df(fit)
out$fit <- list(fit)
return(out)
}
fit
}
predict.serial_recall_pars <- function(object, data, group_by, type = "response", ...) {
if (missing(group_by)) {
pred <- switch(type,
"response" = serial_recall_v2(
setsize = nrow(data),
ISI = data$ISI,
item_in_ltm = data$item_in_ltm,
prop = object["prop"],
prop_ltm = object["prop_ltm"],
tau = object["tau"],
gain = object["gain"],
rate = object["rate"],
prim_prop = object["prim_prop"],
...
),
"strength" = serial_recall_strength(
setsize = nrow(data),
ISI = data$ISI,
item_in_ltm = data$item_in_ltm,
prop = object["prop"],
prop_ltm = object["prop_ltm"],
tau = object["tau"],
gain = object["gain"],
rate = object["rate"],
...
)
)
return(pred)
}
by <- do.call(paste, c(data[, group_by], sep = "_"))
out <- lapply(split(data, by), function(x) {
x$pred_tmp_col295 <- predict(object, x, type = type, ...)
x
})
out <- do.call(rbind, out)
out <- suppressMessages(dplyr::left_join(data, out))
out$pred_tmp_col295
}
```
One example fit:
```{r}
#| message: false
set.seed(25)
fit <- estimate_model(c(start_fun(), prim_prop = rbeta(1, 5, 2)), exp3_data_agg, version = 2, exclude_sp1 = T)
kableExtra::kable(optimfit_to_df(fit))
exp3_data_agg$pred <- predict(fit, exp3_data_agg, group_by = c("chunk", "gap"))
exp3_data_agg |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)
```
Run the estimation 100 times with different starting values:
```{r}
set.seed(18)
fits <- run_or_load(
{
res <- replicate(
n = 100,
expr = estimate_model(
c(start_fun(), prim_prop = rbeta(1, 5, 2)),
exp3_data_agg,
version = 2, exclude_sp1 = T
),
simplify = FALSE
)
res <- do.call(rbind, lapply(res, optimfit_to_df))
arrange(res, deviance)
},
file = "output/exp3_fits_100_prop_primacy.rds"
)
```
Refine the fits with a second pass starting from the best fit:
```{r}
fits_refined <- run_or_load(
{
res <- apply(fits, 1, function(x) {
fit <- estimate_model(x, exp3_data_agg, version = 2, exclude_sp1 = T)
optimfit_to_df(fit)
})
do.call(rbind, res)
},
file = "output/exp3_fits_100_prop_primacy_refined.rds"
)
fits_refined$deviance <- 2 * fits_refined$deviance
```
Print fits sorted by deviance:
```{r}
kableExtra::kable(arrange(fits_refined, deviance))
```
Not as much variance as I thought there would be. Let's limit to the fits within 2 deviance units of the best fit:
Here is the distribution of parameter values that are within 2 deviance units of the best fit:
```{r}
best_fits <- filter(fits_refined, deviance < min(deviance) + 2)
best_fits |>
select(prop:prim_prop) |>
pivot_longer(cols = everything(), names_to = "parameter", values_to = "value") |>
ggplot(aes(x = value)) +
geom_histogram(bins = 30) +
facet_wrap(~parameter, scales = "free") +
theme_pub()
```
Here is the plot of the best fitting model:
```{r}
best_fit <- estimate_model(unlist(best_fits[1, 1:6]), exp3_data_agg, version = 2, exclude_sp1 = T)
exp3_data_agg$pred <- predict(best_fit, exp3_data_agg, group_by = c("chunk", "gap"))
exp3_data_agg |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)
```
and the parameter estimates:
```{r}
kableExtra::kable(t(as.data.frame(best_fit$par)))
```
with this rate, the resource recovery over time looks like this:
```{r}
resources <- function(R, rate, time, r_max = 1) {
(r_max - R) * (1 - exp(-rate * time))
}
time <- seq(0, 20, 0.1)
tibble(time = time, resources = resources(0, best_fits[1, ]$rate, time)) |>
ggplot(aes(x = time, y = resources)) +
geom_line() +
theme_pub()
```
with 50% of the resource recovered after `r round(-log(0.5) / best_fits[1,]$rate, 2)` seconds
and 25% of the resource recovered after `r round(-log(0.75) / best_fits[1,]$rate, 2)` seconds
## Simulate full trial sequences
### With recovery during entire recall period
Calculate the total recall period duration on each trial:
```{r}
#| label: recall_times
#| fig-width: 5
#| fig-height: 4
total_rts <- exp3_data |>
group_by(id, trial) |>
summarize(total_recall_duration = sum(rt) + 9 * 0.2 + 1)
hist(total_rts$total_recall_duration, breaks = 30, col = "grey", border = "white", xlab = "Total recall period duration (s.)", main = "")
```
Create the trial structure for the simulation:
```{r}
#| label: trial_structure
#| message: false
exp3_trial_str <- run_or_load({
exp3_data |>
group_by(id, trial) |>
do({
aggregate_data(.)
})
}, file = "output/exp3_trial_structure.rds")
exp3_trial_str <- left_join(exp3_trial_str, total_rts) |>
mutate(ISI = ifelse(itemtype == "SP7-9", total_recall_duration, ISI),
ser_pos = case_when(
itemtype == "SP1-3" ~ 1,
itemtype == "SP4-6" ~ 2,
itemtype == "SP7-9" ~ 3
))
```
Run the model without resetting the resource at the start of each trial:
```{r}
#| label: sim_no_reset
#| message: false
serial_recall_full <- function(
setsize, ISI = rep(0.5, setsize), item_in_ltm = rep(TRUE, setsize), ser_pos = 1:setsize,
prop = 0.2, prop_ltm = 0.5, tau = 0.15, gain = 25, rate = 0.1, prim_prop = 1,
r_max = 1, lambda = 1, growth = "linear") {
R <- r_max
p_recall <- vector("numeric", length = setsize)
prop_ltm <- ifelse(item_in_ltm, prop_ltm, 1)
for (item in 1:setsize) {
# strength of the item and recall probability
strength <- (prop * R)^lambda * prim_prop^(ser_pos[item] - 1)
p_recall[item] <- 1 / (1 + exp(-(strength - tau) * gain))
# amount of resources consumed by the item
r_cost <- strength^(1 / lambda) * prop_ltm[item]
R <- R - r_cost
# recover resources
R <- switch(growth,
"linear" = min(r_max, R + rate * ISI[item]),
"asy" = R + (r_max - R) * (1 - exp(-rate * ISI[item]))
)
}
p_recall
}
subj1 <- exp3_trial_str |>
filter(id == 44125)
```
Here it is for one example subject:
::: {.column-screen}
```{r}
#| message: false
#| fig-width: 12
#| fig-height: 4
subj1$pred <- serial_recall_full(
setsize = nrow(subj1),
ISI = subj1$ISI,
item_in_ltm = subj1$item_in_ltm,
ser_pos = subj1$ser_pos,
prop = best_fit$par["prop"],
prop_ltm = best_fit$par["prop_ltm"],
tau = best_fit$par["tau"],
gain = best_fit$par["gain"],
rate = best_fit$par["rate"],
prim_prop = best_fit$par["prim_prop"],
growth = "asy"
)
subj1 |>
ungroup() |>
mutate(absolute_position = 1:n()) |>
ggplot(aes(x = absolute_position, y = pred)) +
geom_point() +
geom_line() +
theme_pub()
```
:::
Same, but collapsed over serial position (one value per trial):
```{r}
#| message: false
subj1 |>
ungroup() |>
ggplot(aes(x = trial, y = pred)) +
stat_summary(geom = "point") +
geom_smooth() +
theme_pub()
```
Now simulate the full dataset:
```{r}
#| label: sim_no_reset_full
#| message: false
sim_no_reset_full <- function(data, best_fit) {
data |>
group_by(id) |>
mutate(pred = serial_recall_full(
setsize = n(),
ISI = ISI,
item_in_ltm = item_in_ltm,
ser_pos = ser_pos,
prop = best_fit$par["prop"],
prop_ltm = best_fit$par["prop_ltm"],
tau = best_fit$par["tau"],
gain = best_fit$par["gain"],
rate = best_fit$par["rate"],
prim_prop = best_fit$par["prim_prop"],
growth = "asy"
))
}
full_sim <- sim_no_reset_full(exp3_trial_str, best_fit)
ggplot(full_sim, aes(x = trial, y = pred)) +
stat_summary() +
geom_smooth() +
theme_pub()
```
Yes, the model predicts worsening performance over trials, but the effect is miniscule.
Plot the original predictions recomputed with the full trial-by-trial model:
```{r}
#| message: false
full_sim |>
group_by(chunk, gap, itemtype) |>
summarize(pred = mean(pred),
p_correct = mean(p_correct)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)
```
### No recovery during recall, except during empty screens
```{r}
exp3_trial_str <- run_or_load(
{
exp3_data |>
group_by(id, trial) |>
do({
aggregate_data(.)
})
},
file = "output/exp3_trial_structure.rds"
)
exp3_trial_str <- exp3_trial_str |>
mutate(
ISI = ifelse(itemtype == "SP7-9", 9 * 0.2 + 1, ISI),
ser_pos = case_when(
itemtype == "SP1-3" ~ 1,
itemtype == "SP4-6" ~ 2,
itemtype == "SP7-9" ~ 3
)
)
full_sim_v2 <- sim_no_reset_full(exp3_trial_str, best_fit)
ggplot(full_sim_v2, aes(x = trial, y = pred)) +
stat_summary() +
theme_pub()
filter(full_sim_v2, id == 44125) |>
mutate(absolute_position = 1:n()) |>
ggplot(aes(x = absolute_position, y = pred)) +
geom_point() +
geom_line() +
theme_pub()
```
```{r}
#| message: false
full_sim_v2 |>
group_by(chunk, gap, itemtype) |>
summarize(pred = mean(pred),
p_correct = mean(p_correct)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point(alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, linewidth = 0.5) +
geom_line(aes(y = pred), linetype = "dashed", linewidth = 1.1) +
scale_color_discrete("First chunk LTM?") +
facet_wrap(~itemtype)
```