Code
library(tidyverse)
library(targets)
library(GGally)
library(kableExtra)
tar_source()In the initial modeling notebook, I discovered some problems with parameter identifiability. Here I will explore this issue further.
Initially I ran the model described in the May 13, 2024 draft with 100 different starting parameters. Here are 5 sets of very different best-fitting parameters that produce nearly identical fits as measured by the negative log-likelihood (deviance):
| prop | prop_ltm | rate | tau | gain | deviance | |
|---|---|---|---|---|---|---|
| set1 | 0.098 | 0.815 | 0.006 | 0.084 | 96.954 | 40.377 |
| set2 | 0.132 | 0.818 | 0.009 | 0.108 | 54.078 | 40.429 |
| set3 | 0.155 | 0.820 | 0.010 | 0.123 | 40.135 | 40.491 |
| set4 | 0.173 | 0.822 | 0.011 | 0.133 | 32.738 | 40.556 |
| set5 | 0.215 | 0.826 | 0.013 | 0.154 | 21.967 | 40.772 |
We can see that they all produce nearly identical predictions (the lines are the model predictions, the points are the data):
fits |>
mutate(pred = map2(fit, data, \(x, y) predict(x, y, group_by = c("chunk", "gap")))) |>
unnest(c(data, pred)) |>
mutate(gap = as.factor(gap)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, linetype = set, group = interaction(chunk, set))) +
scale_color_discrete("First chunk LTM?") +
scale_linetype_discrete("Parameter set") +
facet_grid(~itemtype) +
theme_pub()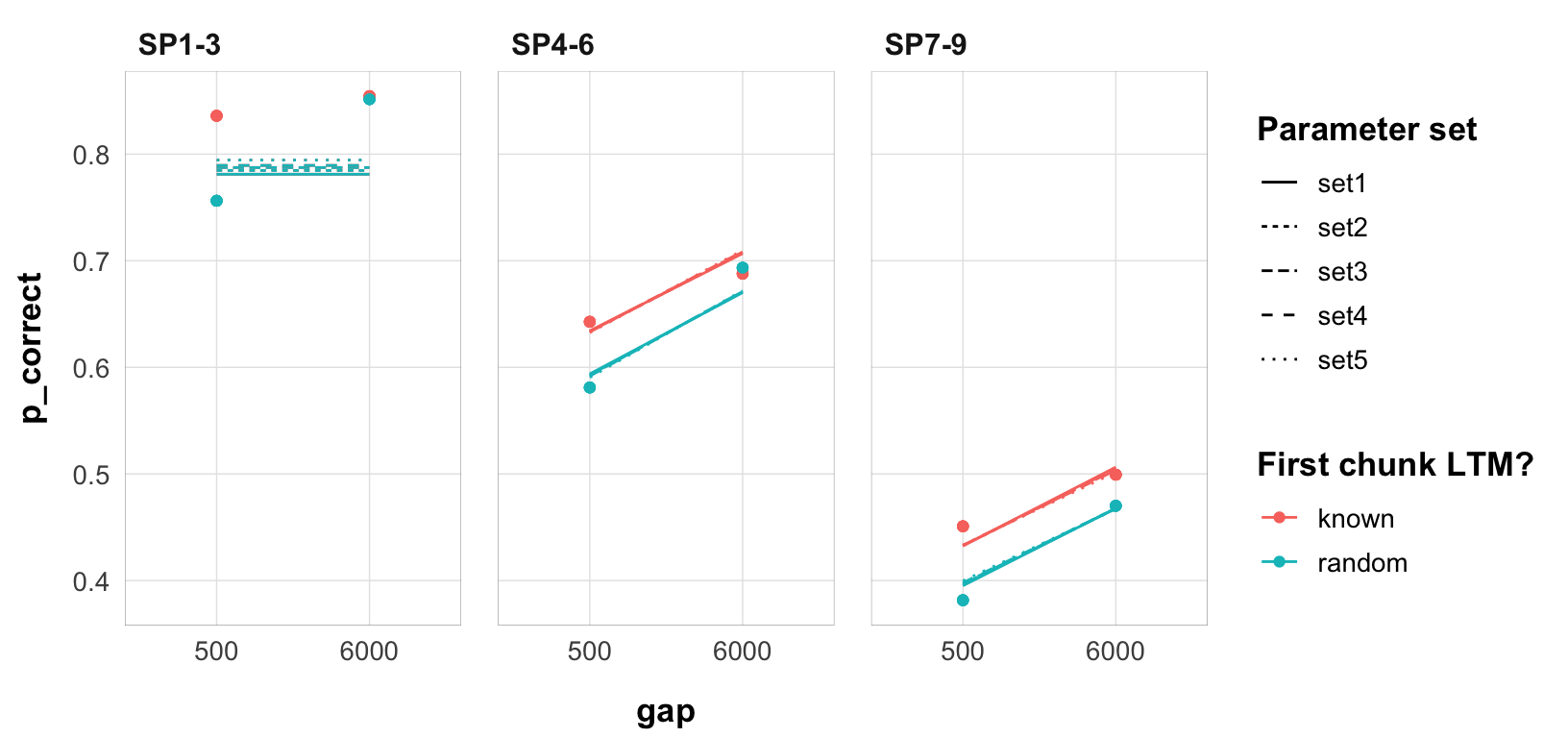
The plot below shows the strong nearly linear trade-offs between the parameters.
I ran a simulation in which I fix1 the rate parameter to values in the range 0.005 to 0.2. I want to see if the identical fits extend to higher rates.
We first extract the best-fitting parameters for each rate from the 100 random start fits.
tar_load(fits2)
fits2 <- fits2 |>
mutate(
deviance = pmap_dbl(list(fit, data, exclude_sp1), function(x, y, z) {
overall_deviance(x$par, data = y, exclude_sp1 = z)
}),
rate = round(rate, 3)
)
best <- fits2 |>
group_by(rate, exp, exclude_sp1) |>
filter(deviance == min(deviance)) |>
slice(1) |>
select(rate, prop, prop_ltm, tau, gain, deviance, fit, data) |>
mutate(pred = map2(fit, data, \(x, y) predict(x, y, group_by = c("chunk", "gap")))) |>
ungroup()Adding missing grouping variables: `exp`, `exclude_sp1`subset for exp2 and exclude_sp1 = TRUE
From the deviance it’s already clear that the fits get wose once we get above 0.020 rate. Here are the best-fitting parameters for each rate:
| rate | prop | prop_ltm | tau | gain | deviance |
|---|---|---|---|---|---|
| 0.005 | 0.098 | 0.812 | 0.084 | 100.000 | 42.689 |
| 0.010 | 0.155 | 0.819 | 0.121 | 41.585 | 40.518 |
| 0.015 | 0.235 | 0.826 | 0.159 | 19.374 | 40.871 |
| 0.020 | 0.316 | 0.835 | 0.183 | 11.537 | 41.687 |
| 0.025 | 0.389 | 0.841 | 0.194 | 8.143 | 43.185 |
| 0.030 | 0.451 | 0.844 | 0.197 | 6.359 | 45.610 |
| 0.035 | 0.496 | 0.842 | 0.197 | 5.394 | 49.069 |
| 0.040 | 0.528 | 0.834 | 0.196 | 4.765 | 53.434 |
| 0.045 | 0.324 | 0.465 | 0.210 | 8.718 | 57.907 |
| 0.050 | 0.355 | 0.459 | 0.220 | 7.359 | 58.648 |
| 0.055 | 0.384 | 0.455 | 0.228 | 6.362 | 59.535 |
| 0.060 | 0.412 | 0.448 | 0.234 | 5.559 | 60.563 |
| 0.065 | 0.439 | 0.442 | 0.239 | 4.955 | 61.729 |
| 0.070 | 0.466 | 0.438 | 0.244 | 4.430 | 63.027 |
| 0.075 | 0.271 | 0.452 | 0.198 | 12.494 | 63.309 |
| 0.080 | 0.272 | 0.457 | 0.199 | 12.582 | 63.309 |
| 0.085 | 0.271 | 0.464 | 0.200 | 12.799 | 63.309 |
| 0.090 | 0.271 | 0.470 | 0.200 | 12.950 | 63.309 |
| 0.095 | 0.271 | 0.476 | 0.201 | 13.072 | 63.309 |
| 0.100 | 0.271 | 0.481 | 0.202 | 13.233 | 63.309 |
A few observations:
Here’s a pairs plot with colors indicating the rate group. The plot indicates that the parameter space does not have a smooth gradient, but rather jumps between regions when rate is fixed to different values.
best_subset <- best_subset |>
mutate(par_groups = case_when(
rate <= 0.02 ~ "0.005-0.02",
rate <= 0.04 ~ "0.025-0.04",
rate <= 0.07 ~ "0.045-0.07",
TRUE ~ "0.07-0.2"
))
best_subset |>
select(prop, prop_ltm, rate, tau, gain, par_groups) |>
ggpairs(
aes(color = par_groups),
diag = list(continuous = "blankDiag"),
upper = list(continuous = "points")
) +
theme_pub() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))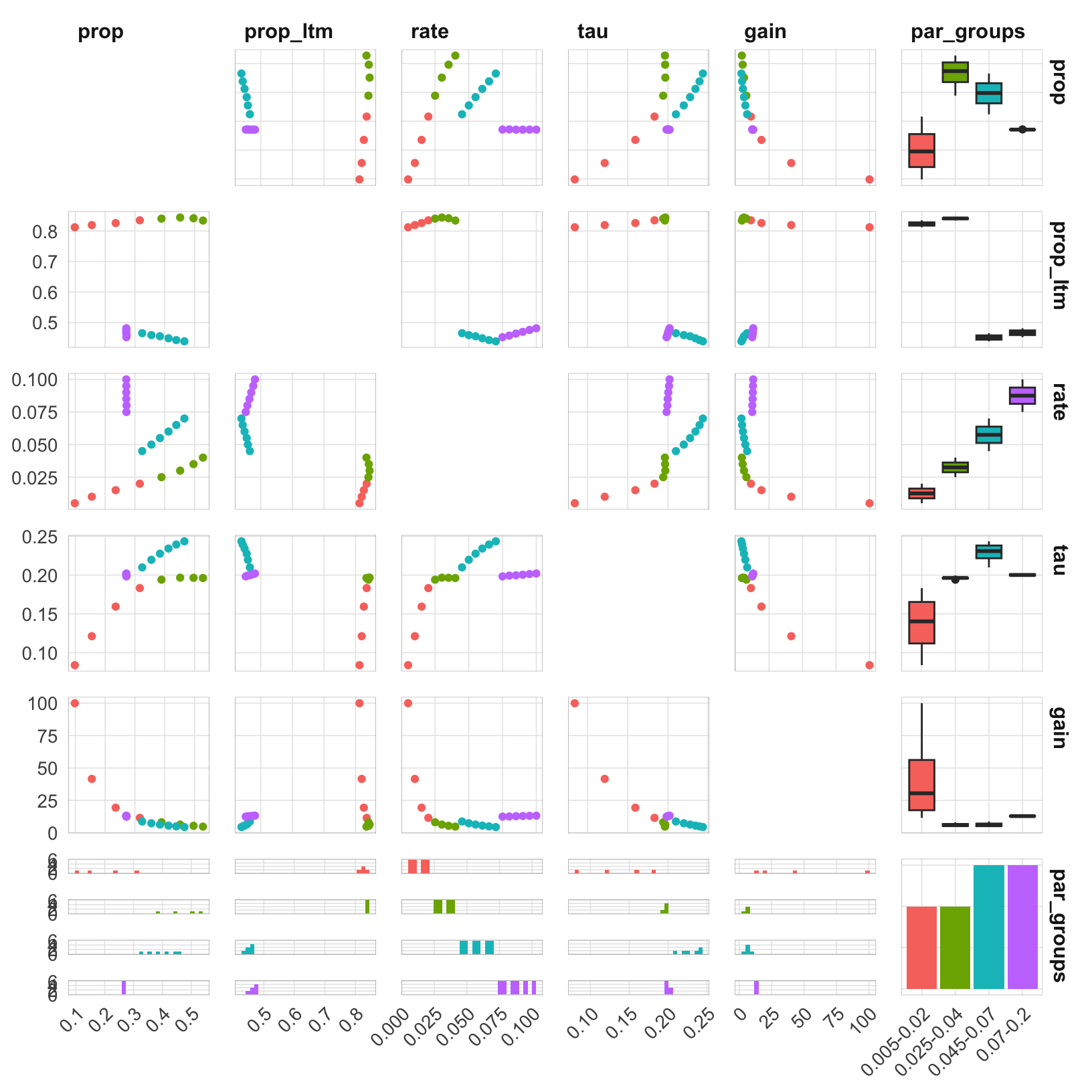
Let’s see how this affects the predictions for the different rate groups. It would be too much to plot all the predictions, so I will first plot the predictions for the first and last parameters for each rate group.
best_subset |>
group_by(par_groups) |>
slice(c(1, n())) |>
unnest(c(data, pred)) |>
mutate(
gap = as.factor(gap),
rate = as.factor(round(rate, 3))
) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, linetype = par_groups, group = interaction(chunk, rate))) +
scale_color_discrete("First chunk LTM?") +
scale_linetype_discrete("Rate") +
facet_grid(rate ~ itemtype) +
theme_pub()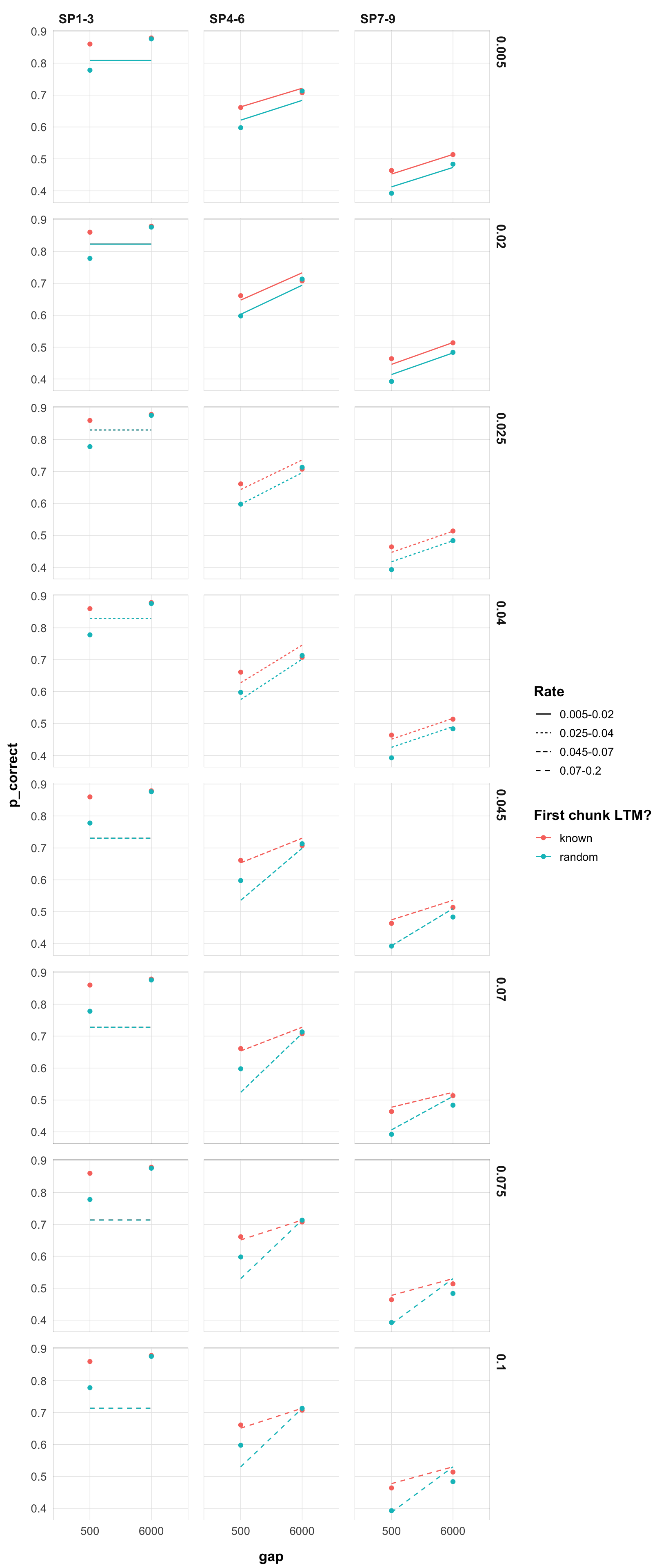
A few observations:
I will now include SP1-3 in the fits and see if this changes the parameter space.
Here are the best-fitting parameters for each rate:
| rate | prop | prop_ltm | tau | gain | deviance |
|---|---|---|---|---|---|
| 0.005 | 0.109 | 0.875 | 0.091 | 92.939 | 119.499 |
| 0.010 | 0.216 | 0.869 | 0.149 | 24.963 | 114.013 |
| 0.015 | 0.303 | 0.867 | 0.176 | 13.406 | 110.780 |
| 0.020 | 0.374 | 0.863 | 0.189 | 9.213 | 109.681 |
| 0.025 | 0.432 | 0.860 | 0.193 | 7.153 | 110.370 |
| 0.030 | 0.481 | 0.859 | 0.193 | 5.961 | 112.559 |
| 0.035 | 0.527 | 0.857 | 0.191 | 5.106 | 116.055 |
| 0.040 | 0.567 | 0.853 | 0.187 | 4.514 | 120.700 |
| 0.045 | 0.602 | 0.853 | 0.183 | 4.074 | 126.391 |
| 0.050 | 0.640 | 0.852 | 0.177 | 3.679 | 133.024 |
| 0.055 | 0.667 | 0.853 | 0.172 | 3.429 | 140.578 |
| 0.060 | 0.697 | 0.852 | 0.166 | 3.181 | 148.930 |
| 0.065 | 0.723 | 0.852 | 0.161 | 2.992 | 158.062 |
| 0.070 | 0.749 | 0.851 | 0.155 | 2.811 | 167.905 |
| 0.075 | 0.773 | 0.853 | 0.148 | 2.660 | 178.428 |
| 0.080 | 0.793 | 0.854 | 0.143 | 2.537 | 189.595 |
| 0.085 | 0.816 | 0.852 | 0.136 | 2.405 | 201.389 |
| 0.090 | 0.836 | 0.854 | 0.130 | 2.300 | 213.730 |
| 0.095 | 0.855 | 0.855 | 0.124 | 2.203 | 226.585 |
| 0.100 | 0.873 | 0.855 | 0.118 | 2.115 | 239.930 |
This now looks much more stable. Until 0.130 we don’t have switchest in the parameter region. Still, rates 0.005-0.03 are very similar.
Here are the plots for rates 0.005-0.10:
pred_data <- best_subset |>
unnest(c(data, pred)) |>
mutate(
gap = as.factor(gap),
rate = round(rate, 3)
)
myplot <- function(data) {
ggplot(data, aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, group = chunk)) +
scale_color_discrete("First chunk LTM?") +
facet_grid(rate ~ itemtype) +
theme_pub()
}I will now repeat the same analysis for experiment 1.
| rate | prop | prop_ltm | tau | gain | deviance |
|---|---|---|---|---|---|
| 0.005 | 0.106 | 0.573 | 0.089 | 100.000 | 36.273 |
| 0.010 | 0.115 | 0.576 | 0.096 | 85.610 | 31.959 |
| 0.015 | 0.170 | 0.579 | 0.129 | 40.879 | 32.380 |
| 0.020 | 0.223 | 0.587 | 0.154 | 24.841 | 33.079 |
| 0.025 | 0.270 | 0.593 | 0.172 | 17.465 | 34.078 |
| 0.030 | 0.314 | 0.600 | 0.184 | 13.397 | 35.384 |
| 0.035 | 0.351 | 0.602 | 0.192 | 11.022 | 37.002 |
| 0.040 | 0.384 | 0.605 | 0.197 | 9.416 | 38.918 |
| 0.045 | 0.413 | 0.607 | 0.200 | 8.305 | 41.117 |
| 0.050 | 0.439 | 0.608 | 0.202 | 7.448 | 43.575 |
| 0.055 | 0.457 | 0.603 | 0.204 | 6.888 | 46.274 |
| 0.060 | 0.481 | 0.603 | 0.205 | 6.310 | 49.177 |
| 0.065 | 0.497 | 0.598 | 0.206 | 5.889 | 52.249 |
| 0.070 | 0.510 | 0.594 | 0.207 | 5.570 | 55.470 |
| 0.075 | 0.405 | 0.374 | 0.221 | 7.375 | 56.971 |
| 0.080 | 0.423 | 0.369 | 0.225 | 6.802 | 58.529 |
| 0.085 | 0.441 | 0.367 | 0.228 | 6.311 | 60.169 |
| 0.090 | 0.457 | 0.364 | 0.230 | 5.910 | 61.889 |
| 0.095 | 0.474 | 0.360 | 0.232 | 5.534 | 63.682 |
| 0.100 | 0.490 | 0.357 | 0.234 | 5.222 | 65.541 |
similar switch at 0.075 to a different region of the parameter space.
Here are the plots for rates 0.005-0.10:
so even a rate of 0.07 does not necessarily predict a big interaction
technically, I put a really narrow prior Normal(value, 0.0001) on the rate parameter rather than fixing it just because I can do it in the existing code.↩︎
---
title: "Parameter identifiability"
format:
html:
html-table-processing: none
---
## Overview
```{r}
#| label: init
#| message: false
library(tidyverse)
library(targets)
library(GGally)
library(kableExtra)
tar_source()
```
In [the initial modeling notebook](modelling_edas_approach.qmd#problem-with-parameter-identifiability), I discovered some problems with parameter identifiability. Here I will explore this issue further.
Initially I ran the model described in the May 13, 2024 draft with 100 different starting parameters. Here are 5 sets of very different best-fitting parameters that produce nearly identical fits as measured by the negative log-likelihood (deviance):
```{r}
#| label: parsets
fits <- readRDS("output/five_parsets_exp2.rds")
fits$set <- paste0("set", 1:5)
fits[, 1:6] |>
as.data.frame() |>
`rownames<-`(fits$set) |>
kbl() %>%
kable_styling()
```
We can see that they all produce nearly identical predictions (the lines are the model predictions, the points are the data):
```{r}
#| label: plot five fits
#| fig-width: 8.5
#| fig-height: 4
fits |>
mutate(pred = map2(fit, data, \(x, y) predict(x, y, group_by = c("chunk", "gap")))) |>
unnest(c(data, pred)) |>
mutate(gap = as.factor(gap)) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, linetype = set, group = interaction(chunk, set))) +
scale_color_discrete("First chunk LTM?") +
scale_linetype_discrete("Parameter set") +
facet_grid(~itemtype) +
theme_pub()
```
The plot below shows the strong nearly linear trade-offs between the parameters.
```{r}
#| label: plot par correlations
#| fig-width: 8.5
#| fig-height: 8.5
fits |>
select(prop, rate, tau, gain) |>
ggpairs(
diag = list(continuous = "blankDiag"),
upper = list(continuous = "points")
) +
theme_pub() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
```
## Fix rate to different values and explore the parameter space
I ran a simulation in which I fix[^1] the rate parameter to values in the range 0.005 to 0.2. I want to see if the identical fits extend to higher rates.
[^1]: technically, I put a really narrow prior Normal(value, 0.0001) on the rate parameter rather than fixing it just because I can do it in the existing code.
We first extract the best-fitting parameters for each rate from the 100 random start fits.
```{r}
#| label: rate scan
tar_load(fits2)
fits2 <- fits2 |>
mutate(
deviance = pmap_dbl(list(fit, data, exclude_sp1), function(x, y, z) {
overall_deviance(x$par, data = y, exclude_sp1 = z)
}),
rate = round(rate, 3)
)
best <- fits2 |>
group_by(rate, exp, exclude_sp1) |>
filter(deviance == min(deviance)) |>
slice(1) |>
select(rate, prop, prop_ltm, tau, gain, deviance, fit, data) |>
mutate(pred = map2(fit, data, \(x, y) predict(x, y, group_by = c("chunk", "gap")))) |>
ungroup()
```
subset for exp2 and exclude_sp1 = TRUE
```{r}
#| label: subset best
best_subset <- filter(best, exp == 2, exclude_sp1)
```
From the deviance it's already clear that the fits get wose once we get above 0.020 rate. Here are the best-fitting parameters for each rate:
```{r}
#| label: best fits
best_subset |>
select(rate, prop, prop_ltm, tau, gain, deviance) |>
mutate_all(round, 3) |>
kbl() %>%
kable_styling()
```
A few observations:
1) with recovery rates higher than 0.07 the fits do no change much
2) when the rate changes from 0.04 to 0.045, we switch to a different region of the parameter space. Similarly from 0.065 to 0.07
3) looks like we have four ranges of rates with qualitative shifts:
- ***0.005 to 0.02:*** the fits are very similar and prop_ltm is ~ 0.8. The other parameters change proportionally to the rate
- ***0.025 to 0.04:*** fits get progressively worse. the other parameters still changes similarly to the first group, but tau is not stable. Seems like tau can no longer compensate, leading to worsening fits
- ***0.045 to 0.07:*** prop_ltm drops to ~0.45 and stays there. The other parameters again change proportionally to the rate, but they are now in a different region of the parameter space. Fits gradually worsen as we increase the rates
- ***0.07 to 0.2:*** prop is now stable at ~0.255. The other parameters change but with very small increments. Fits are identical
Here's a pairs plot with colors indicating the rate group. The plot indicates that the parameter space does not have a smooth gradient, but rather jumps between regions when rate is fixed to different values.
```{r}
#| label: plot rate correlations
#| message: false
#| fig-width: 8.5
#| fig-height: 8.5
best_subset <- best_subset |>
mutate(par_groups = case_when(
rate <= 0.02 ~ "0.005-0.02",
rate <= 0.04 ~ "0.025-0.04",
rate <= 0.07 ~ "0.045-0.07",
TRUE ~ "0.07-0.2"
))
best_subset |>
select(prop, prop_ltm, rate, tau, gain, par_groups) |>
ggpairs(
aes(color = par_groups),
diag = list(continuous = "blankDiag"),
upper = list(continuous = "points")
) +
theme_pub() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
```
Let's see how this affects the predictions for the different rate groups. It would be too much to plot all the predictions, so I will first plot the predictions for the first and last parameters for each rate group.
```{r}
#| label: plot rate fits
#| fig-width: 8.5
#| fig-height: 20
best_subset |>
group_by(par_groups) |>
slice(c(1, n())) |>
unnest(c(data, pred)) |>
mutate(
gap = as.factor(gap),
rate = as.factor(round(rate, 3))
) |>
ggplot(aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, linetype = par_groups, group = interaction(chunk, rate))) +
scale_color_discrete("First chunk LTM?") +
scale_linetype_discrete("Rate") +
facet_grid(rate ~ itemtype) +
theme_pub()
```
A few observations:
- Rates above 0.045 lead to the same fit, because they cause full recovery from first item to the second with 6 s ISI. We can see that from he plots because the prediction for SP1-3 and sp4-6 (6000 ISI) are the same for all rates above 0.045, meaning no serial position effect from the first to the second chunk. This is completely implausible, so we can rule out rates above 0.045.
### Including SP1-3 in the fits
I will now include SP1-3 in the fits and see if this changes the parameter space.
```{r}
#| label: include sp1
best_subset <- filter(best, exp == 2, exclude_sp1 == FALSE)
```
Here are the best-fitting parameters for each rate:
```{r}
#| label: best fits sp1
best_subset |>
select(rate, prop, prop_ltm, tau, gain, deviance) |>
mutate_all(round, 3) |>
kbl() %>%
kable_styling()
```
This now looks much more stable. Until 0.130 we don't have switchest in the parameter region. Still, rates 0.005-0.03 are very similar.
Here are the plots for rates 0.005-0.10:
```{r}
#| label: plot rate fits sp1
#| fig-width: 8.5
#| fig-height: 20
pred_data <- best_subset |>
unnest(c(data, pred)) |>
mutate(
gap = as.factor(gap),
rate = round(rate, 3)
)
myplot <- function(data) {
ggplot(data, aes(x = gap, y = p_correct, color = chunk)) +
geom_point() +
geom_line(aes(y = pred, group = chunk)) +
scale_color_discrete("First chunk LTM?") +
facet_grid(rate ~ itemtype) +
theme_pub()
}
```
::: {.panel-tabset}
## Rate [0.005, 0.025]
```{r}
#| label: plot rate fits sp1 1
#| fig-width: 8
#| fig-height: 12
myplot(filter(pred_data, rate < 0.026))
```
## Rate [0.03, 0.05]
```{r}
#| label: plot rate fits sp1 2
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate < 0.051 & rate > 0.029))
```
## Rate [0.055, 0.75]
```{r}
#| label: plot rate fits sp1 3
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate < 0.076 & rate > 0.054))
```
## Rate [0.08, 0.10]
```{r}
#| label: plot rate fits sp1 4
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate > 0.079, rate < 0.101))
```
:::
## What about experiment 1?
I will now repeat the same analysis for experiment 1.
```{r}
#| label: exp1
best_subset <- filter(best, exp == 1, exclude_sp1)
best_subset |>
select(rate, prop, prop_ltm, tau, gain, deviance) |>
mutate_all(round, 3) |>
kbl() %>%
kable_styling()
```
similar switch at 0.075 to a different region of the parameter space.
Here are the plots for rates 0.005-0.10:
```{r}
#| label: plot rate fits exp1
#| fig-width: 8.5
#| fig-height: 20
pred_data <- best_subset |>
unnest(c(data, pred)) |>
mutate(
gap = as.factor(gap),
rate = round(rate, 3)
)
```
::: {.panel-tabset}
## Rate [0.005, 0.025]
```{r}
#| label: plot rate fits 1 (exp1)
#| fig-width: 8
#| fig-height: 12
myplot(filter(pred_data, rate < 0.026))
```
## Rate [0.03, 0.05]
```{r}
#| label: plot rate fits 2 (exp1)
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate < 0.051 & rate > 0.029))
```
## Rate [0.055, 0.75]
```{r}
#| label: plot rate fits 3 (exp1)
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate < 0.076 & rate > 0.054))
```
## Rate [0.08, 0.10]
```{r}
#| label: plot rate fits 4 (exp1)
#| fig-width: 8
#| fig-height: 12
#| message: false
myplot(filter(pred_data, rate > 0.079, rate < 0.101))
```
:::
so even a rate of 0.07 does not necessarily predict a big interaction
## Summary
- The parameter space is not smooth, but rather jumps between regions when rate is fixed to different values
- There are ridges in the parameter space where the fits are very similar